Question

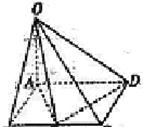在四棱锥O-ABCD中，OA⊥平面ABCD，底面ABCD为矩形，AB=OA=tBC（t＞0）．
（I）当t=1时，求证：BD⊥DC；
（II）若BC边有且仅有一个点E，使得OE⊥ED，求此时二面角A-CD-E的正切值．

Answer 1

分析：（I）t=1?底面ABCD为正方形?BD⊥AC?BD⊥面OAC?BD⊥OC
（II）由AB，AD，AO两两垂直，分别以它们所在直线为x轴、y轴、z轴建立坐标系，令AB=1?BC=

1

t

，设BE=m，由BC边上有且仅有一个点E，使得OE⊥ED时，E为BC的中点，且t=

1

2

，m=1，再分别求得面OED的法向量与平面OAD的法向量，用向量夹角公式求得二面角．

解答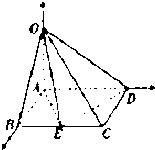：解：（I）当t=1时底面ABCD为正方形，
∴BD⊥AC
又因为BD⊥OA，∴BD⊥面OAC
又OC?面OAC，∴BD⊥OC（5分）
（II）因为AB，AD，AO两两垂直，分别以它们所在
直线为x轴、y轴、z轴建立坐标系，如图所示，令AB=1，
可得BC=

1

t

则B（1，0，0），D(0，

1

t

，0)，C(1，

1

t

，0)，O(0，0，1)（7分）
设BE=m，则E（1，m，0）(0≤m≤

1

t

)
要使OE⊥ED，只要

OE

•

ED

=-1+m(

1

t

-m)=0即tm²-m+t=0
∵BC边有且仅有一个点E，使得OE⊥ED．∴△=0?t=

1

2

，此时m=1．
所以BC边上有且仅有一个点E，使得OE⊥ED时，E为BC的中点，且t=

1

2

（9分）
设面OED的法向量

p

=（x，y，1）
则

p • ED =0 p • DO =0

即

-x+y=0 -2y+1=0

解得

p

=(

1

2

，

1

2

，1)
取平面OAD的法向量

q

=（1，0，0）则（

p

•

q

）的大小与二面角A-DO-E的大小相等或互补．
所以cos＜

p

•

q

＞=

6

6

．
因此二面角A-OD-E的正切值为

5

．（12分）

点评：本题主要考查线线，线面，面面垂直关系的转化和向量法求二面角问题．