题目内容
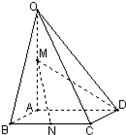
 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=| π | 4 |
(1)求三棱锥B-OCD的体积;
(2)求异面直线AB与MD所成角的大小;
注:若直线a⊥平面α,则直线a与平面α内的所有直线都垂直.
分析:(1)由题意判断OA为三棱锥O-BCD的高,利用三棱锥的换底性,计算三棱锥O-BCD的体积;
(2)连接MC,可证∠CDM为异面直线AB与MD所成的角,在△CDM中,分别求出三边长,利用余弦定理计算角的余弦值,进而求得角的大小.
(2)连接MC,可证∠CDM为异面直线AB与MD所成的角,在△CDM中,分别求出三边长,利用余弦定理计算角的余弦值,进而求得角的大小.
解答:解:(1)∵OA⊥底面ABCD,∴OA为三棱锥O-BCD的高,OA=2,
在△BCD中,∠BCD=
,
∴S△BCD=
×1×1×
=
,
∴VB-OCD=VO-BCD=
×
×2=
;
(2)连接MC,
∵AB∥CD,∴∠CDM为异面直线AB与MD所成的角,
∵∠ABC=
,∴AC=
,
∴CM2=1+2-
=3-
;DM=
,CD=1,
∴cos∠CDM=
=
,
∴∠CDM=
.
故异面直线AB与MD所成的角为
.
在△BCD中,∠BCD=
| 3π |
| 4 |
∴S△BCD=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
∴VB-OCD=VO-BCD=
| 1 |
| 3 |
| ||
| 4 |
| ||
| 6 |
(2)连接MC,
∵AB∥CD,∴∠CDM为异面直线AB与MD所成的角,
∵∠ABC=
| π |
| 4 |
1+1-2×1×1×
|
2-
|
∴CM2=1+2-
| 2 |
| 2 |
| 2 |
∴cos∠CDM=
1+2-3+
| ||
2×1×
|
| 1 |
| 2 |
∴∠CDM=
| π |
| 3 |
故异面直线AB与MD所成的角为
| π |
| 3 |

点评:本题考查了利用三棱锥的换底性求三棱锥的体积,考查了异面直线所成角的定义及求法,考查了学生的空间想象能力与运算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题
如图,在四棱锥O-ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC中点,以A为原点,建立适当的空间直角坐标系,利用空间向量解答以下问题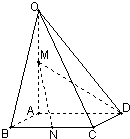 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC=
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,∠ABC= 如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,
如图,在四棱锥O-ABCD中,底面ABCD四边长为1的菱形,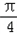 ,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.
,OA⊥底面ABCD,OA=2,M为OA的中点,N为BC的中点.