题目内容
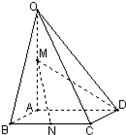
16、如图，在四棱锥O-ABCD中，AD∥BC，AB=AD=2BC，OB=OD，M是OD的中点．求证：（Ⅰ）直线MC∥平面OAB；
（Ⅱ）直线BD⊥直线OA．
分析：（1）设N是OA的中点，连接MN，NB，依据题设条件证明四边形MNBC是平行四边形，以得到直线MC∥平面OAB的条件，用线面平行的判定定理证之；
（2）设H是BD的中点，连接AH，OH，在这个等腰三角形中证明BD与AH，OH垂直，下用线面垂直的判定定理证明．
（2）设H是BD的中点，连接AH，OH，在这个等腰三角形中证明BD与AH，OH垂直，下用线面垂直的判定定理证明．
解答：证明：（1）设N是OA的中点，连接MN，NB，
因为M是OD的中点，
所以MN∥AD，且2MN=AD，
又AD∥BC，AD=2BC，
所以MNBC是平行四边形，
所以MC∥NB，
又MC 不在平面OAB上，NB?平面OAB，
所以直线MC∥平面OAB；（7分）
（2）设H是BD的中点，连接AH，
因为AB=AD，所以AH⊥BD，
又因为OB=OD，所以OH⊥BD
所以BD⊥面OAH
所以BD⊥OA、（14分）
因为M是OD的中点，
所以MN∥AD，且2MN=AD，
又AD∥BC，AD=2BC，
所以MNBC是平行四边形，
所以MC∥NB，
又MC 不在平面OAB上，NB?平面OAB，
所以直线MC∥平面OAB；（7分）
（2）设H是BD的中点，连接AH，
因为AB=AD，所以AH⊥BD，
又因为OB=OD，所以OH⊥BD
所以BD⊥面OAH
所以BD⊥OA、（14分）
点评：考查线面平行的判定定理与线面垂直的判定定理，知识性较强，在每一小题中，亦可用面面平行来证明线面平行，请读者看看如何构造这个平面．
练习册系列答案
相关题目
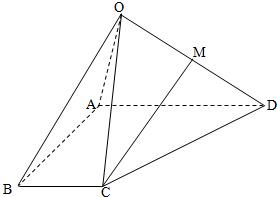
如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC中点，以A为原点，建立适当的空间直角坐标系，利用空间向量解答以下问题
如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，∠ABC=
如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，
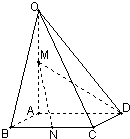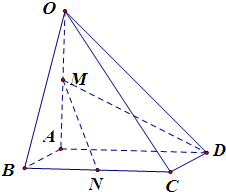
如图，在四棱锥O-ABCD中，底面ABCD四边长为1的菱形，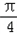
，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC的中点．