题目内容
某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交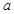 元(
元(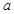 为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与
为常数,2≤a≤5 )的税收。设每件产品的售价为x元(35≤x≤41),根据市场调查,日销售量与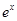 (e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(e为自然对数的底数)成反比例。已知每件产品的日售价为40元时,日销售量为10件。
(1)求该商店的日利润L(x)元与每件产品的日售价x元的函数关系式;
(2)当每件产品的日售价为多少元时,该商品的日利润L(x)最大,并求出L(x)的最大值。
(1) 
(2) 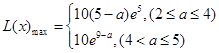
解析试题分析:解(1)设日销售量为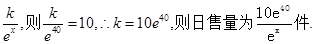 2分
2分
则日利润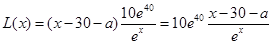 4分
4分
(2)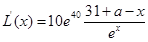 7分
7分 ①当2≤a≤4时,33≤a+31≤35,当35 <x<41时,
①当2≤a≤4时,33≤a+31≤35,当35 <x<41时,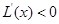
∴当x=35时,L(x)取最大值为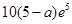 10分
10分
②当4<a≤5时,35≤a+31≤36,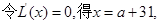
易知当x=a+31时,L(x)取最大值为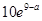 13分
13分
综合上得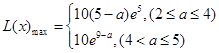 - 14分
- 14分
考点:函数模型的运用
点评:解决的关键是利用函数的单调性来判定最值,求解得到,属于基础题。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 的图像顶点为
的图像顶点为 ,且图像在x轴上截得线段长为8
,且图像在x轴上截得线段长为8
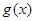 在
在 上是单调增函数,求实数
上是单调增函数,求实数 的取值范围;
的取值范围;  若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和.
若不建隔热层(即x=0时),每年能源消耗费用为8万元.设f(x)为隔热层建造费用与20年的能源消耗费用之和. (其中
(其中 为大于0的常数),在
为大于0的常数),在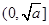 上是减函数,在
上是减函数,在 上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值.
上是增函数”这一性质,求隔热层修建多厚时,总费用f(x)达到最小,并求出这个最小值. 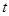 表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于
表示时间,以月为单位,年初为起点,根据历年数据,某水库的蓄水量(单位:亿立方米)关于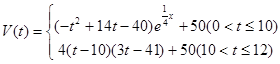
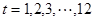 ),问:同一年内哪些月份是枯水期?
),问:同一年内哪些月份是枯水期?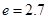 计算)
计算)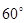 (如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为
(如图),考虑到防洪堤坚固性及石块用料等因素,设计其断面面积为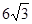 平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段
平方米,为了使堤的上面与两侧面的水泥用料最省,则断面的外周长(梯形的上底线段 与两腰长的和)要最小.
与两腰长的和)要最小.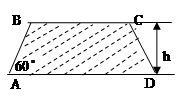
 的范围内,外周长最小为多少米?
的范围内,外周长最小为多少米? .已知甲、乙两地相距100千米。
.已知甲、乙两地相距100千米。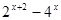
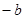 =0.
=0.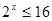 且
且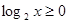 ,求实数b的取值范围.
,求实数b的取值范围.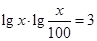 .
.