题目内容
18.已知在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,他们的终边分别与单位圆交于A,B,A,B的横坐标分别为$\frac{\sqrt{2}}{10}$,$\frac{2\sqrt{5}}{5}$,则α+2β的值为$\frac{3π}{4}$.分析 由条件利用任意角的三角函数的定义求得cosα、cosβ 的值,再利用同角三角函数的基本关系求得 sinα、sinβ 的值,再利用二倍角公式求得sin2β、cos2β 的值,可得α+2β∈(0,π).利用两角和的余弦公式求得cos(α+2β)的值,可得α+2β的值.
解答 解:由题意可得cosα=$\frac{\sqrt{2}}{10}$,cosβ=$\frac{2\sqrt{5}}{5}$,∴sinα=$\sqrt{{1-cos}^{2}α}$=$\frac{7\sqrt{2}}{10}$,sinβ=$\sqrt{{1-cos}^{2}β}$=$\frac{\sqrt{5}}{5}$,
∴sin2β=2sinβcosβ=$\frac{4}{5}$,cos2β=2cos2β-1=$\frac{3}{5}$,∴2β仍为锐角,α+2β∈(0,π).
∴cos(α+2β)=cosαcos2β-sinαsin2β=$\frac{\sqrt{2}}{10}×\frac{3}{5}$-$\frac{7\sqrt{2}}{10}×\frac{4}{5}$=-$\frac{\sqrt{2}}{2}$,
∴α+2β=$\frac{3π}{4}$.
点评 本题主要考查任意角的三角函数的定义,同角三角函数的基本关系,二倍角公式、两角和的余弦公式的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
13.下列不等式的解集为空集的是( )
| A. | |x-1|≤0 | B. | x2-x+4>0 | C. | |1-x|<-4 | D. | x2-2x+1≤0 |
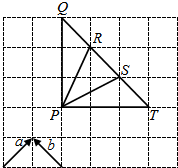 如图所示,下列结论正确的是( )
如图所示,下列结论正确的是( )