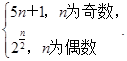题目内容
设不等式组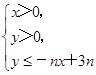 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,且Tn=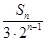 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
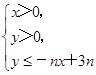 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).(1)求数列{an}的通项公式;
(2)记数列{an}的前n项和为Sn,且Tn=
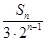 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.(1)an=3n(n∈N*)(2)m≥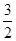 .
.
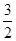 .
.(1)由x>0,y>0,3n-nx>0,得0<x<3.
∴x=1,或x=2.∴Dn内的整点在直线x=1和x=2上.
记直线y=-nx+3n为l,l与直线x=1、x=2的交点的纵坐标分别为y1,y2.
则y1=-n+3n=2n,y2=-2n+3n=n.∴an=3n(n∈N*).
(2)∵Sn=3(1+2+3+…+n)=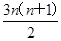 ,
,
∴Tn=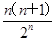 ,∴Tn+1-Tn=
,∴Tn+1-Tn=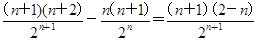 ,
,
∴当n≥3时,Tn>Tn+1,且T1=1<T2=T3=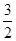 .
.
于是T2,T3是数列{Tn}中的最大项,故m≥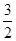 .
.
∴x=1,或x=2.∴Dn内的整点在直线x=1和x=2上.
记直线y=-nx+3n为l,l与直线x=1、x=2的交点的纵坐标分别为y1,y2.
则y1=-n+3n=2n,y2=-2n+3n=n.∴an=3n(n∈N*).
(2)∵Sn=3(1+2+3+…+n)=
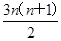 ,
,∴Tn=
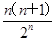 ,∴Tn+1-Tn=
,∴Tn+1-Tn=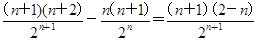 ,
,∴当n≥3时,Tn>Tn+1,且T1=1<T2=T3=
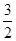 .
.于是T2,T3是数列{Tn}中的最大项,故m≥
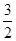 .
.
练习册系列答案
相关题目
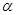 为锐角,且
为锐角,且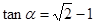 ,函数
,函数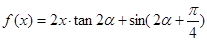 ,数列
,数列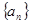 的首项
的首项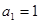 ,
,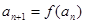 .
.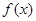 的表达式;(2)求数列
的表达式;(2)求数列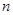 项和
项和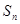 .
.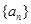 的前
的前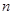 项和为
项和为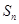 ,
,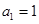 ,且
,且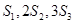 成等差数列.
成等差数列.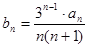 ,求数列
,求数列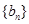 的前
的前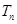 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有
 为常数,且
为常数,且 .
. ,数列
,数列 满足
满足
 ,
, ,求数列
,求数列 的通项公式;
的通项公式; 的前
的前 .
.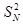 -(n2+n-1)Sn-(n2+n)=0.
-(n2+n-1)Sn-(n2+n)=0.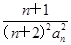 ,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<
,数列{bn}的前n项和为Tn.证明:对于任意的n∈N*,都有Tn<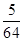 .
.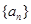 的前n项和为
的前n项和为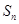 ,且
,且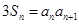 ,则
,则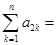 ( )
( )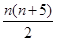
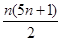
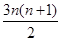

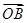 =a100·
=a100·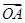 +a101
+a101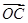 ,且A、B、C三点共线(该直线不过点O),则S200=________.
,且A、B、C三点共线(该直线不过点O),则S200=________.