题目内容
【题目】已知:正三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() 为棱
为棱![]() 的中点.
的中点.

(![]() )求证:
)求证: ![]() 平面
平面![]() .
.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析:(1)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,由三棱柱
,由三棱柱![]() 为正三棱柱及
为正三棱柱及![]() 为棱
为棱![]() 的中点,可得
的中点,可得![]() ∥
∥![]() ,即可证明
,即可证明![]() ∥平面
∥平面![]() ;(2)根据正三棱柱的定义,可证
;(2)根据正三棱柱的定义,可证![]() ,
, ![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() ;(3)先求底面
;(3)先求底面![]() 的面积,再求高
的面积,再求高![]() ,即可求出四棱锥的体积.
,即可求出四棱锥的体积.
试题解析:(1)连结![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]()
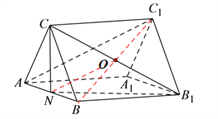
∵三棱柱![]() 为正三棱柱
为正三棱柱
∴![]() 为
为![]() 的中点
的中点
∵![]() 为棱
为棱![]() 的中点
的中点
∴![]() ∥
∥![]()
∵![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() ∥平面
∥平面![]()
(2)∵三棱柱![]() 为正三棱柱
为正三棱柱
∴三角形![]() 为正三角形,侧棱
为正三角形,侧棱![]() 平面
平面![]()
∵![]() 为棱
为棱![]() 的中点,
的中点, ![]() 平面
平面![]()
∴![]() ,
, ![]()
∵![]() ,
, ![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]()
∵![]() 平面
平面![]()
∴平面![]() 平面
平面![]()
(3)∵![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]()
∴四边形![]() 的面积为
的面积为![]()
∵![]() 平面
平面![]()
∴四棱锥![]() 的体积为
的体积为![]()

练习册系列答案
相关题目