题目内容
在半径为R的半球内有一内接圆柱,则这个圆柱的体积的最大值是( )
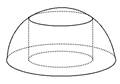

A.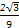 πR3 πR3 | B.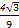 πR3 πR3 |
C.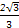 πR3 πR3 | D. πR3 πR3 |
A
设圆柱的高为h,则圆柱的底面半径为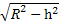 ,圆柱的体积为V=π(R2-h2)h=-πh3+πR2h(0<h<R),V'=-3πh2+πR2=0,则h=
,圆柱的体积为V=π(R2-h2)h=-πh3+πR2h(0<h<R),V'=-3πh2+πR2=0,则h=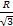 时V有最大值为V=
时V有最大值为V=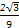 πR3.
πR3.
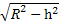 ,圆柱的体积为V=π(R2-h2)h=-πh3+πR2h(0<h<R),V'=-3πh2+πR2=0,则h=
,圆柱的体积为V=π(R2-h2)h=-πh3+πR2h(0<h<R),V'=-3πh2+πR2=0,则h=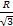 时V有最大值为V=
时V有最大值为V=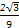 πR3.
πR3.
练习册系列答案
相关题目
 平面ABC,
平面ABC, ,
,

 ,
, 表示三棱锥A-CBE的体积,求函数
表示三棱锥A-CBE的体积,求函数 的正方体
的正方体 中,点
中,点 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且满足
上,且满足 .
.
 ;
; 上确定一点
上确定一点 ,使
,使 、
、 的长;
的长; 的体积.
的体积.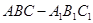 中,
中,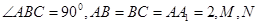 分别是
分别是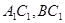 的中点.
的中点.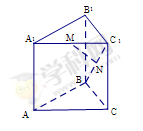
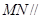 平面
平面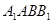 ;
; 的体积.
的体积. 的圆柱的侧面积为( )
的圆柱的侧面积为( )



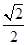 ,
,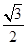 ,
,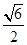 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )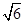 π
π ,则该三棱锥的外接球的表面积是( )
,则该三棱锥的外接球的表面积是( )


