题目内容
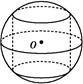
已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,则球O的表面积为 .
如图,设截面小圆的半径为r,球的半径为R,因为AH∶HB=1∶2,所以OH=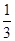 R.由勾股定理,有R2=r2+OH2,
R.由勾股定理,有R2=r2+OH2,
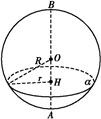
又由题意得πr2=π,则r=1,故R2=1+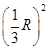 ,即R2=
,即R2=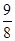 .由球的表面积公式,得S=4πR2=
.由球的表面积公式,得S=4πR2=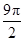 .
.
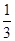 R.由勾股定理,有R2=r2+OH2,
R.由勾股定理,有R2=r2+OH2,
又由题意得πr2=π,则r=1,故R2=1+
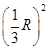 ,即R2=
,即R2=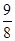 .由球的表面积公式,得S=4πR2=
.由球的表面积公式,得S=4πR2=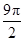 .
.
练习册系列答案
相关题目
 中,
中,
 底面
底面 ,
, ,
, ,
,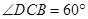 .
.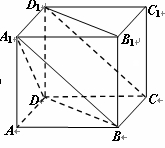
 平面
平面 ;
; ,求四棱锥
,求四棱锥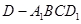 的体积.
的体积.

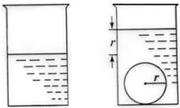
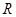 的圆柱形量杯中装有适量的水若放入一个半径为
的圆柱形量杯中装有适量的水若放入一个半径为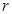 的实心铁球,水面高度恰好升高
的实心铁球,水面高度恰好升高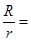 ____________.
____________.
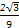 πR3
πR3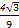 πR3
πR3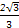 πR3
πR3 πR3
πR3