题目内容
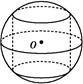
如图所示,半径为4的球O中有一内接圆柱,当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是 .

32π
法一 设球的半径与圆柱的高所成的角为α,
则圆柱底面半径为4sinα,高为8cosα,
∴S圆柱侧=2π·4sinα·8cosα=32πsin2α.
当sin2α=1时,S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
法二 设圆柱底面半径为r,则其高为2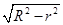 ,
,
∴S圆柱侧=2πr·2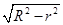 =4π
=4π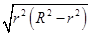 ≤
≤
4π =2πR2
=2πR2
(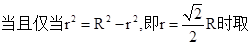 “=”).
“=”).
又R=4,∴S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
则圆柱底面半径为4sinα,高为8cosα,
∴S圆柱侧=2π·4sinα·8cosα=32πsin2α.
当sin2α=1时,S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.
法二 设圆柱底面半径为r,则其高为2
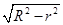 ,
,∴S圆柱侧=2πr·2
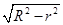 =4π
=4π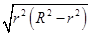 ≤
≤4π
 =2πR2
=2πR2(
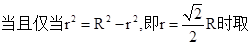 “=”).
“=”).又R=4,∴S圆柱侧最大为32π.
此时S球表-S圆柱侧=4π·42-32π=32π.

练习册系列答案
相关题目
 A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
A1B1C1中,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF= AB.
AB.
 的正方体
的正方体 中,点
中,点 是棱
是棱 的中点,点
的中点,点 在棱
在棱 上,且满足
上,且满足 .
.
 ;
; 上确定一点
上确定一点 ,使
,使 、
、 的长;
的长; 的体积.
的体积. 中侧棱垂直于底面,
中侧棱垂直于底面, ,
, ,
, ,且三棱柱
,且三棱柱 ,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
,AD=2,求四边形ABCD绕AD旋转一周所成几何体的表面积及体积.
 A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P
A1B1C1D1的棱长为2,动点E,F在棱A1B1上,点Q是棱CD的中点,动点P在棱AD上.若EF=1,DP=x,A1E=y(x,y大于零),则三棱锥P