题目内容
【题目】在平面直角坐标系xOy中,点A(2,0),点B在单位圆上,∠AOB=θ(0<θ<π).
(1)若点B(﹣ ![]() ,
, ![]() ),求tan(
),求tan( ![]() ﹣θ)的值;
﹣θ)的值;
(2)若 ![]() ,
, ![]()
![]() =
= ![]() ,求cos(
,求cos( ![]() +θ)的值.
+θ)的值.
【答案】
(1)解:若 ![]() ,如图:
,如图:
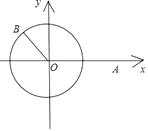
则: ![]() ;
;
∴ ![]() ;
;
∴ 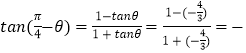 7;
7;
(2)解: ![]() ;
;
∴ ![]() ;
;
∴ ![]() =
= ![]() ;
;
∴ ![]() ;
;
又θ∈(0,π);
∴ ![]() ;
;
∴ ![]()
= ![]()
= ![]() .
.
【解析】(1)B点坐标为 ![]() 时,可画出图形,从而可得出sinθ,cosθ的值,进而得出tanθ的值,这样根据两角差的正切公式便可求出
时,可画出图形,从而可得出sinθ,cosθ的值,进而得出tanθ的值,这样根据两角差的正切公式便可求出 ![]() 的值;(2)根据条件可得到
的值;(2)根据条件可得到 ![]() ,从而可表示出
,从而可表示出 ![]() 的坐标,进行数量积的坐标运算便可由
的坐标,进行数量积的坐标运算便可由 ![]() 得出cosθ的值,进而求出sinθ的值,从而便可求出
得出cosθ的值,进而求出sinθ的值,从而便可求出 ![]() 的值.
的值.

练习册系列答案
相关题目

