题目内容
【题目】设 
是等差数列， 
是各项都为正数的等比数列，且 
， 
， 
（1）求数列 ， 的通项公式；
（2）设数列 
的前 
项和为 
试比较 与6的大小.
【答案】
（1）解：设 
的公差为 
， 
的公比为 
．
则依题意有 
且 
，
解得 
，
所以 
， 
．
（2）解： 
，
，①
，②
②-①得： 
．
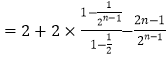
【解析】(1)由题意结合等差数列和等比数列的定义求出公差和公比进而得到两个数列的通项公式。(2)根据题意整理出通项公式求出前n项和的公式，再利用等式两边乘以公比后两式相减即可求出前n项和的公式，整理该式即得到一个等比数列，根据等比数列求和公式即可求出结果。
【考点精析】解答此题的关键在于理解等差数列的前n项和公式的相关知识，掌握前n项和公式：
，以及对等比数列的定义的理解，了解如果一个数列从第2项起，每一项与它的前一项的比等于同一个常数，那么这个数列就叫做等比数列．
练习册系列答案
名校课堂系列答案
相关题目
