题目内容
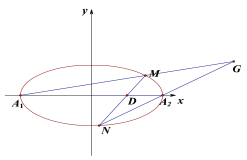
【题目】直角坐标系xoy中,椭圆![]() 的离心率为
的离心率为![]() ,过点
,过点![]() .
.
(1)求椭圆C的方程;
(2)已知点P(2,1),直线![]() 与椭圆C相交于A,B两点,且线段AB被直线OP平分.
与椭圆C相交于A,B两点,且线段AB被直线OP平分.
①求直线![]() 的斜率;②若
的斜率;②若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1) ![]() .
.
(2) ①直线![]() 的斜率为除
的斜率为除![]() 以外的任意实数.
以外的任意实数.
②![]() .
.
【解析】分析:(1)由离心率条件得![]() ,然后将点
,然后将点![]() .代入原式得到第二个方程,联立求解即可;(2)①先得出OP的方程
.代入原式得到第二个方程,联立求解即可;(2)①先得出OP的方程![]() ,然后根据点差法研究即可;②先表示出
,然后根据点差法研究即可;②先表示出![]() ,然后联立直线和椭圆根据韦达定理代入等式求解即可.
,然后联立直线和椭圆根据韦达定理代入等式求解即可.
详解:
(1)由![]() 可得
可得![]() ,
,
设椭圆方程为![]() ,代入点
,代入点![]() ,得
,得![]() ,
,
故椭圆方程为:![]() .
.
(2)①由条件知![]() ,
,
设![]() ,则满足
,则满足![]() ,
,![]() ,
,
两式作差得:![]() ,
,
化简得![]() ,
,
因为![]() 被
被![]() 平分,故
平分,故![]() ,
,
当![]() 即直线
即直线![]() 不过原点时,
不过原点时,![]() ,所以
,所以![]() ;
;
当![]() 即直线
即直线![]() 过原点时,
过原点时,![]() ,
,![]() 为任意实数,但
为任意实数,但![]() 时
时![]() 与
与![]() 重合;
重合;
综上即直线![]() 的斜率为除
的斜率为除![]() 以外的任意实数.
以外的任意实数.
②当![]() 时,
时,![]() ,故
,故![]()
![]() ,
,
得![]() ,联立
,联立![]() ,得
,得![]() ,舍去;
,舍去;
当![]() 时,设直线
时,设直线![]() 为
为![]() ,代入椭圆方程
,代入椭圆方程![]() 可得
可得![]() ,(#)
,(#)
所以![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
故![]()
![]()
解得![]() ,此时方程(#)中
,此时方程(#)中![]() ,
,
故所求直线方程为![]() .
.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目