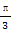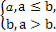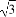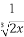题目内容
若存在过点(1,0)的直线与曲线y=x3和y=ax2+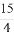 x-9都相切,则a等于( )
x-9都相切,则a等于( )
(A)-1或-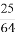 (B)-1或
(B)-1或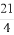
(C)- 或-
或-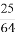 (D)-
(D)- 或7
或7
A
【解析】【思路点拨】先设出切点坐标,再根据导数的几何意义写出切线方程,最后由点(1,0)在切线上求出切点后再求a的值.
解:设过点(1,0)的直线与曲线y=x3相切于点(x0,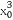 ),所以切线方程为y-
),所以切线方程为y-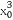 =3
=3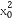 (x-x0),
(x-x0),
即y=3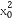 x-2
x-2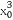 .
.
又(1,0)在切线上,则x0=0或x0=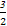 ,
,
当x0=0时,由y=0与y=ax2+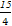 x-9相切可得Δ=(
x-9相切可得Δ=(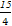 )2-4a(-9)=0,
)2-4a(-9)=0,
解得a=-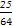 ,
,
同理,当x0=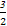 时,由y=
时,由y= x-
x- 与y=ax2+
与y=ax2+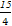 x-9相切可得a=-1,所以选A.
x-9相切可得a=-1,所以选A.
【方法技巧】导数几何意义的应用
导数的几何意义是切点处切线的斜率,应用时主要体现在以下几个方面:
(1)已知切点A(x0,f(x0))求斜率k,即求该点处的导数值:k=f'(x0).
(2)已知斜率k,求切点A(x1,f(x1)),即解方程f'(x1)=k.
(3)已知过某点M(x1,f(x1))(不是切点)的切线斜率为k时,常需设出切点A(x0,f(x0)),利用k= 求解.
求解.

练习册系列答案
相关题目