题目内容
【题目】如图，已知
为等边三角形，
为等腰直角三角形，
.平面
平面ABD，点E与点D在平面ABC的同侧，且
，
.点F为AD中点，连接EF.
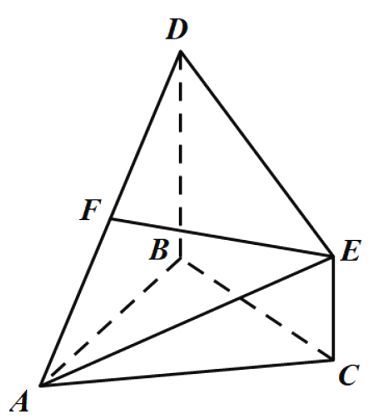
（1）求证：
平面ABC；
（2）求证：平面
平面ABD.
【答案】（1）见详解；（2）见详解
【解析】
（1）取
的中点
，连接
，可证出
，由线面平行的判定定理即可证出；
（2）首先证出
平面ABD，再由（1）可证得
平面ABD，根据面面垂直的判定定理即可证出.
（1）
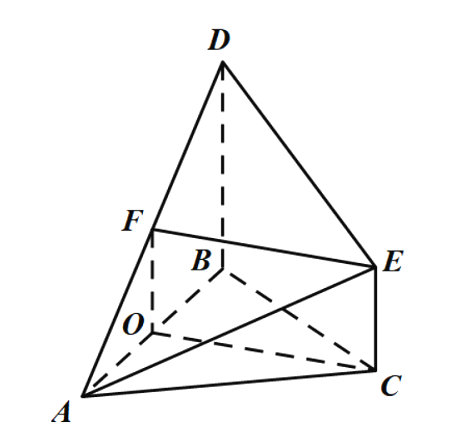
取的中点，连接，
点F为AD中点，
且
，
，
且
，
四边形
为平行四边形，
,
又因为
平面ABC，
平面ABC，
所以
平面ABC.
（2）由（1）点为的中点，且
为等边三角形，
所以
，
又因为
.平面
平面ABD，
所以
平面ABC，所以
,
又
，所以平面ABD，
又
，所以平面ABD，
平面AED，
平面
平面ABD. 
津桥教育计算小状元系列答案
【题目】已知某产品的销售额
与广告费用
之间的关系如下表：
| 0 | 1 | 2 | 3 | 4 |
| 10 | 15 |
| 30 | 35 |
若根据表中的数据用最小二乘法求得对的回归直线方程为
，则下列说法中错误的是（ ）
A.产品的销售额与广告费用成正相关
B.该回归直线过点
C.当广告费用为10万元时，销售额一定为74万元
D.
的值是20
【题目】某市《城市总体规划（
年）》提出到
年实现“
分钟社区生活圈”全覆盖的目标，从教育与文化、医疗与养老、交通与购物、休闲与健身
个方面构建“分钟社区生活圈”指标体系，并依据“分钟社区生活圈”指数高低将小区划分为：优质小区（指数为
）、良好小区（指数为
）、中等小区（指数为
）以及待改进小区（指数为
）个等级.下面是三个小区个方面指标的调查数据：
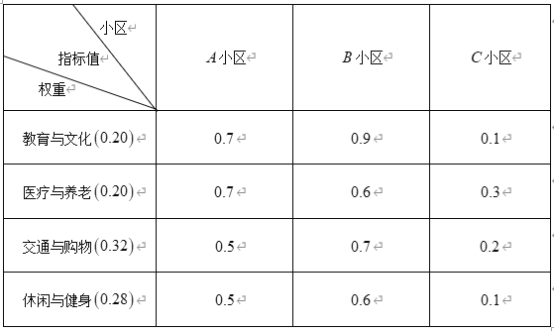
注：每个小区“分钟社区生活圈”指数
，其中
、
、
、
为该小区四个方面的权重，
、
、
、
为该小区四个方面的指标值（小区每一个方面的指标值为
之间的一个数值）.
现有
个小区的“分钟社区生活圈”指数数据，整理得到如下频数分布表：
分组 |
|
|
|
|
|
频数 |
|
|
|
|
|
（Ⅰ）分别判断
、
、
三个小区是否是优质小区，并说明理由；
（Ⅱ）对这个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样，抽取
个小区进行调查，若在抽取的个小区中再随机地选取
个小区做深入调查，记这个小区中为优质小区的个数
，求的分布列及数学期望.
【题目】近年来，我国工业经济发展迅速，工业增加值连年攀升，某研究机构统计了近十年（从2008年到2017年）的工业增加值（万亿元），如下表：
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年份序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
工业增加值 | 13.2 | 13.8 | 16.5 | 19.5 | 20.9 | 22.2 | 23.4 | 23.7 | 24.8 | 28 |
依据表格数据，得到下面的散点图及一些统计量的值.
|
|
|
|
|
5.5 | 20.6 | 82.5 | 211.52 | 129.6 |
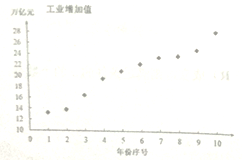
（1）根据散点图和表中数据，此研究机构对工业增加值
（万亿元）与年份序号
的回归方程类型进行了拟合实验，研究人员甲采用函数
，其拟合指数
；研究人员乙采用函数
，其拟合指数
；研究人员丙采用线性函数
，请计算其拟合指数，并用数据说明哪位研究人员的函数类型拟合效果最好.（注：相关系数
与拟合指数
满足关系
）.
（2）根据（1）的判断结果及统计值，建立关于的回归方程（系数精确到0.01）；
（3）预测到哪一年的工业增加值能突破30万亿元大关.
附：样本
的相关系数
，
，
，
.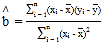