题目内容
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系中,圆C的方程为 (θ为参数).以坐标原点O为极点,
(θ为参数).以坐标原点O为极点, ![]() 轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线
轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线![]() 的极坐标方程
的极坐标方程![]() .
.
(Ⅰ)当![]() 时,判断直线
时,判断直线![]() 与
与![]() 的关系;
的关系;
(Ⅱ)当![]() 上有且只有一点到直线
上有且只有一点到直线![]() 的距离等于
的距离等于![]() 时,求
时,求![]() 上到直线
上到直线![]() 距离为
距离为![]() 的点的坐标.
的点的坐标.
【答案】(1)见解析;(2)(2,0)和(0,2).
【解析】试题分析:(I)将曲线方程化成直角坐标方程,计算圆心到直线的距离与圆的半径比较大小得出结论;
(II)由题意可知直线与圆相离,且圆心到直线l的距离为2![]() ,故到直线l的距离等于2
,故到直线l的距离等于2![]() 的点在过圆心且与直线l平行的直线上,求出此直线的参数方程代入圆的方程求出该点对应的参数,得出该点的坐标.
的点在过圆心且与直线l平行的直线上,求出此直线的参数方程代入圆的方程求出该点对应的参数,得出该点的坐标.
试题解析:
(Ⅰ)圆C的普通方程为:(x-1)2+(y-1) 2=2,
直线l的直角坐标方程为:x+y-3=0,
圆心(1,1)到直线l的距离为![]()
所以直线l与C相交.
(Ⅱ) 直线l的普通方程为x+y﹣m=0.
∵C上有且只有一点到直线l的距离等于![]() ,
,
∴直线l与圆C相离,且圆心到直线的距离为![]() .
.
∴圆C上到直线l的距离等于2![]() 的点在过圆心C(1,1)且与直线l平行的直线上.
的点在过圆心C(1,1)且与直线l平行的直线上.
∴过圆心C(1,1)且与直线l平行的直线的参数方程为: 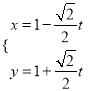 (t为参数).
(t为参数).
将: 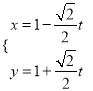 (t为参数)代入圆C的普通方程得t2=2,
(t为参数)代入圆C的普通方程得t2=2,
∴t1=![]() ,t2=﹣
,t2=﹣![]() .
.
当t=![]() 时,
时, ![]() ,当t=﹣
,当t=﹣![]() 时,
时, ![]() .
.
∴C上到直线l距离为2![]() 的点的坐标为(0,2),(2,0).
的点的坐标为(0,2),(2,0).

练习册系列答案
相关题目



