题目内容

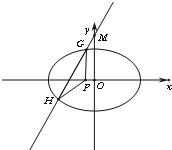
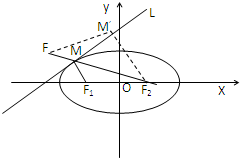
在直线l：x-y+9=0上任取一点M，过M作以F1（-3，0），F2（3，0）为焦点的椭圆，当M在什么位置时，所作椭圆长轴最短？并求此椭圆方程．
设F1（-3，0）关于l：x-y+9=0的对称点F（x，y）
则
x-3
2
-
y
2
+9=0
y-0
x+3
=-1
⇒
x=-9
y=6
，即F（-9，6），
连F2F交l于M，点M即为所求．
F2F：y=-
1
2
(x-3)即x+2y-3=0
解方程组
x+2y-3=0
x-y+9=0
⇒
x=-5
y=4
，即M（-5，4）
当点M′取异于M的点时，|FM′|+|M′F2|＞|FF2|．
满足题意的椭圆的长轴2a=|FF2|=
(-9-3)2+62
=6
5

所以a=3
5
，b2=a2-c2=45-9=36
所以椭圆的方程为：
x2
45
+
y2
36
=1．
练习册系列答案
相关题目
已知抛物线C：y2=8x，O为坐标原点，动直线l：y=k（x+2）与抛物线C交于不同两点A，B
（1）求证：
OA
•
OB
为常数；
（2）求满足
OM
=
OA
+
OB
的点M的轨迹方程．
如图，过抛物线y2=2px（p＞0）的焦点F的两条互相垂直的直线与抛物线分别交于点A、B和C、D；抛物线上的点T（2，t）（t＞0）到焦点的距离为3．
（1）求p、t的值；
（2）当四边形ACBD的面积取得最小值时，求直线AB的斜率．
（1）已知△ABC的顶点A（0，-1），B（0，1），直线AC，直线BC的斜率之积等于m（m0），求顶点C的轨迹方程，并判断轨迹为何种圆锥曲线．
（2）已知圆M的方程为：（x+1）2+y2=（2a）2（a＞0，且a1），定点N（1，0），动点P在圆M上运动，线段PN的垂直平分线与直线MP相交于点Q，求点Q轨迹方程．
抛物线C：x2=2py（p＞0）的焦点为F，O为坐标原点；当抛物线上点N的纵坐标为1时，|NF|=2，已知直线l经过抛物线C的焦点F，且与抛物线C交于A，B两点
（1）求抛物线C的方程；
（2）若△AOB的面积为4，求直线l的方程．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
2
2
，直线l：y=x+2与原点为圆心，以椭圆C的短轴长为直径的圆相切．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点M（0，2）的直线l1与椭圆C交于G，H两点．设直线l1的斜率k＞0，在x轴上是否存在点P（m，0），使得△PGH是以GH为底边的等腰三角形．如果存在，求出实数m的取值范围，如果不存在，请说明理由．
已知椭圆
y2
a2
+
x2
b2
=1(a＞b＞0)的离心率e=
3
2
，短轴长为2，点A（x1，y1），B（x2，y2）是椭圆上的两点，
m
=(
x1
b
，
y1
a
)，
n
=(
x2
b
，
y2
a
)，且
m
•
n
=0．
（1）求椭圆方程；
（2）若直线AB过椭圆的焦点F（0，c）（c为半焦距），求直线AB的斜率；
（3）试问：△AOB的面积是否为定值？如果是，请给予证明；如果不是，请说明理由．
如图．已知椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的长轴为AB，过点B的直线l与x轴垂直，椭圆的离心率e=
3
2
，F1为椭圆的左焦点且
AF1
•
F1B
=1．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）设P是椭圆上异于A、B的任意一点，PH⊥x轴，H为垂足，延长HP到点Q使得HP=PQ．连接AQ并延长交直线l于点M，N为MB的中点，判定直线QN与以AB为直径的圆O的位置关系．
已知：椭圆
x2
a2
+
y2
b2
=1（a＞b＞0），过点A（-a，0），B（0，b）的直线倾斜角为
π
6
，原点到该直线的距离为
3
2
．
（1）求椭圆的方程；
（2）斜率大于零的直线过D（-1，0）与椭圆交于E，F两点，若
ED
=2
DF
，求直线EF的方程；
（3）是否存在实数k，直线y=kx+2交椭圆于P，Q两点，以PQ为直径的圆过点D（-1，0）？若存在，求出k的值；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网