题目内容
【题目】已知抛物线![]() 过点
过点![]() ,且P到抛物线焦点的距离为2直线
,且P到抛物线焦点的距离为2直线![]() 过点
过点![]() ,且与抛物线相交于A,B两点.
,且与抛物线相交于A,B两点.
(Ⅰ)求抛物线的方程;
(Ⅱ)若点Q恰为线段AB的中点,求直线![]() 的方程;
的方程;
(Ⅲ)过点![]() 作直线MA,MB分别交抛物线于C,D两点,请问C,D,Q三点能否共线?若能,求出直线
作直线MA,MB分别交抛物线于C,D两点,请问C,D,Q三点能否共线?若能,求出直线![]() 的斜率
的斜率![]() ;若不能,请说明理由.
;若不能,请说明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)能,
;(Ⅲ)能,![]() .
.
【解析】
(Ⅰ)根据题意,结合抛物线的性质,即可求出抛物线的方程为![]() 。
。
(Ⅱ)设![]() ,
,![]() ,设而不求利用点差法求出直线AB的斜率,再利用点斜式即可求出直线
,设而不求利用点差法求出直线AB的斜率,再利用点斜式即可求出直线![]() 的方程。
的方程。
(Ⅲ)设 ,
,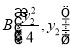 ,
, ,
, ,且
,且![]() .联立直线与抛物线方程,得到联立方程,再利用韦达定理以及M,A,C三点共线得出
.联立直线与抛物线方程,得到联立方程,再利用韦达定理以及M,A,C三点共线得出![]() 的数量关系,假设C,D,Q三点共线,构造关于
的数量关系,假设C,D,Q三点共线,构造关于 ![]() 的等式,转化为
的等式,转化为![]() 的等式,进行求解即可得出结论。
的等式,进行求解即可得出结论。
(Ⅰ)由题意有![]() ,及
,及![]() ,
,
解得![]() .故抛物线的方程为
.故抛物线的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
两式相减得![]() ,即
,即![]() .
.
于是![]() ,
,![]() ,
,
(注:利用直线与抛物线方程联立,求得![]() ,同样得4分)
,同样得4分)
故直线l的方程为![]() ,即
,即![]() ;
;
(Ⅲ)设 ,
,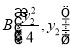 ,
, ,
, ,且
,且![]() .
.
由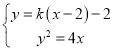 ,得
,得![]() ,则
,则![]() ,
,![]() ,
,
由M,A,C三点共线,可得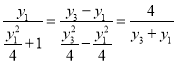 ,化简得
,化简得![]() ,即
,即![]() .
.
同理可得,![]() ,
,
假设C,D,Q三点共线,则有 ,化简得
,化简得![]() ,
,
进一步可得,![]() ,即
,即![]() ,解得
,解得![]() .
.
因此,当直线l的斜率![]() 时,C,D,Q三点共线.
时,C,D,Q三点共线.

练习册系列答案
相关题目