题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,设
时,设![]() 的两个极值点为
的两个极值点为![]() ,
,![]() ,证明:
,证明:![]() .
.
【答案】(1)详见解析(2)证明见解析。
【解析】
(1)利用导函数分子的判别式分情况讨论,即可,注意参数![]() 时,函数图像开口也会发生相应的变化。(2)利用对数平均不等式,证明即可。
时,函数图像开口也会发生相应的变化。(2)利用对数平均不等式,证明即可。
解:(1)![]() ,
,![]() ,
,
对于一元二次方程![]() ,
,![]() ,
,
①当![]() 时,即
时,即![]() 时,
时,![]() 无解或一个解,
无解或一个解,
有![]() 时,
时,![]() ,此时
,此时![]() 在
在![]() 上单调递增,
上单调递增,
②当![]() 时,即
时,即![]() 时,
时,![]() 有两个解,
有两个解,
其解为![]() , 当
, 当![]() 时,
时,![]() ,故在
,故在![]() 及
及![]() 时,
时,![]() ;且
;且![]() 时,
时,![]() ,即
,即![]() 在
在![]() 及
及![]() 上单调递增,在
上单调递增,在![]() 上单调递减,当
上单调递减,当![]() 时,一个实根小于0,一个实根大于0,所以在
时,一个实根小于0,一个实根大于0,所以在![]() 时,
时,![]() ,在
,在![]() ,
,![]() ,即
,即![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
综上所述:即![]() 时,
时,![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,即
时,即![]() 在
在![]() 及
及![]() 上单调递增,在
上单调递增,在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。
上单调递减。
(2)当![]() 时,
时,![]() ,
,![]() ,又因为
,又因为![]() 的两个极值点为
的两个极值点为![]() ,
,![]() ,则
,则![]() ,
,![]() 是方程
是方程![]() 的两实数根,
的两实数根,![]() 设
设![]() 。
。
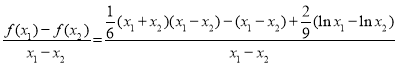

又因为![]() ,故要证
,故要证![]() ,
,
只需证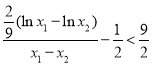 ,
,
只需证![]() ,
,
只需证![]() ,
,
下面证明不等式![]() ,不妨设
,不妨设![]() ,要证
,要证![]() ,即证
,即证![]() ,即证
,即证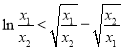 ,令
,令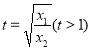 ,设
,设![]() ,则
,则![]() ,所以,函数
,所以,函数![]() 在
在![]() 上递减,而
上递减,而![]() ,因此当
,因此当![]() 时,
时,![]() 恒成立,即
恒成立,即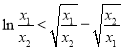 成立,即
成立,即![]() 成立,
成立,
所以 ,得证。
,得证。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目