Question

选修4-1：几何证明选讲
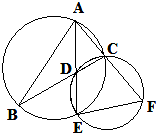
如图，∠BAC的平分线与BC和外接圆分别相交于D和E，延长AC交过D、E、C三点的圆于点F．
（Ⅰ）求证：EF²=ED•EA；
（Ⅱ）若AE=6，EF=3，求AF•AC的值．

Answer 1

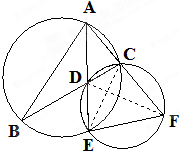（Ⅰ）证明：如图，连接CE，DF．
∵AE平分∠BAC，∴∠BAD=∠DAC…（2分）
在圆内又知∠DCE=∠EFD，∠BCE=∠BAE．∴∠EAF=∠EFD
又∠AEF=∠FED，∴△AEF∽△FED，∴，
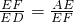∴EF²=ED•EA；
（Ⅱ）由（Ⅰ）知EF²=ED•EA
∵EF=3，AE=6，∴ED=，AD=…（8分）
∴AC•AF=AD•AE=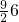=27…（10分）
分析：（Ⅰ）连接CE，DF，证明△AEF∽△FED，即可得到结论；
（Ⅱ）利用相交弦定理，可求AF•AC的值．
点评：本题考查三角形的相似，考查相交弦定理，考查学生分析解决问题的能力，属于中档题．