题目内容
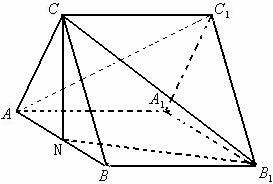
 如图正三棱柱ABC-A1B1C1,
如图正三棱柱ABC-A1B1C1,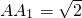 ,AB=2,若N为棱AB中点.
,AB=2,若N为棱AB中点.
(1)求证:AC1∥平面NB1C;
(2)求A1C1与平面NB1C所成的角正弦值.
 证明:(Ⅰ)连接BC1和CB1交于O点,连ON.
证明:(Ⅰ)连接BC1和CB1交于O点,连ON.∵ABC-A1B1C1是正三棱柱,
∴O为BC1的中点.又N为棱AB中点,
∴在△ABC1中,NO∥AC1,又NO?平面NB1C,AC1?平面NB1C,
∴AC1∥平面NB1C;(6分)
(Ⅱ)建如图所示空间直角坐标系,
∵N(0,0,0),
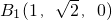 ,
,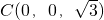 ,
,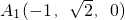 ,
,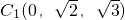 ,
,∴
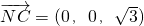 ,
,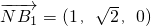
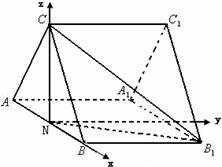 设平面NB1C的法向量为n=(x,y,z),
设平面NB1C的法向量为n=(x,y,z),∴
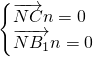 ,即
,即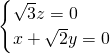 ,
,令
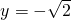 ,得n=
,得n=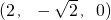 ,
,∵
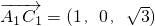 ,
,∴
 ,
,∴A1C1与平面NB1C所成的角正弦值为
 .(13分)
.(13分)分析:(1)求证:AC1∥平面NB1C,连接BC1和CB1交于O点,连ON.只需证明NO∥AC1即可.
(2)求A1C1与平面NB1C所成的角正弦值,利用空间直角坐标系,求出相关向量,求数量积即可求解.
点评:本题考查直线与平面平行的判定,直线与平面所成的角的求法,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图正三棱柱ABC-A1B1C1,
如图正三棱柱ABC-A1B1C1, 如图正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
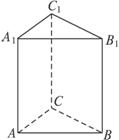 (本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.
(本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.