题目内容
如图正三棱柱ABC-A1B1C1中,底面边长为a,在侧棱BB1上截取BD=
,在侧棱CC1上截取CE=a,过A,D,E作棱柱的截面.
(1)求证:截面ADE⊥侧面ACC1A1;
(2)求截面ADE与底面ABC所成的角.
| a | 2 |
(1)求证:截面ADE⊥侧面ACC1A1;
(2)求截面ADE与底面ABC所成的角.
分析:(1)取AE、AC的中点O、S,连接DO,OS,BS,证明OD⊥侧面ACC1A1,四边形OSBD是矩形,即可证明截面ADE⊥侧面ACC1A1;
(2)利用射影面面积与被射影面面积之比,求出求截面ADE与底面ABC所成的角的余弦值,然后求出角.
(2)利用射影面面积与被射影面面积之比,求出求截面ADE与底面ABC所成的角的余弦值,然后求出角.
解答: 解:(1)证明:取AE、AC的中点O、S,连接DO,OS,BS,
解:(1)证明:取AE、AC的中点O、S,连接DO,OS,BS,
正三棱柱ABC-A1B1C1中,底面边长为a,在侧棱BB1上截取BD=
,
在侧棱CC1上截取CE=a,
易得四边形OSBD是矩形,并且SB⊥侧面ACC1A1,
即OD⊥侧面ACC1A1
所以截面ADE⊥侧面ACC1A1;
(2)截面ADE与底面ABC所成的角为θ
所以cosθ=
=
=
=
θ=45°
 解:(1)证明:取AE、AC的中点O、S,连接DO,OS,BS,
解:(1)证明:取AE、AC的中点O、S,连接DO,OS,BS,正三棱柱ABC-A1B1C1中,底面边长为a,在侧棱BB1上截取BD=
| a |
| 2 |
在侧棱CC1上截取CE=a,
易得四边形OSBD是矩形,并且SB⊥侧面ACC1A1,
即OD⊥侧面ACC1A1
所以截面ADE⊥侧面ACC1A1;
(2)截面ADE与底面ABC所成的角为θ
所以cosθ=
| S△ABC |
| S△ADE |
| ||
|
| AC |
| AE |
| ||
| 2 |
θ=45°
点评:本题考查平面与平面垂直的判定,二面角的求法,考查空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
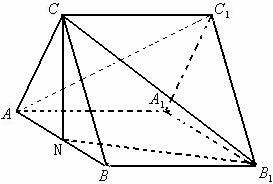 如图正三棱柱ABC-A1B1C1,
如图正三棱柱ABC-A1B1C1, 如图正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
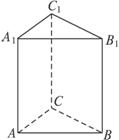 (本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.
(本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.