题目内容
侧棱垂直于底面且底面是正三角形的三棱柱叫做正三棱柱;如图正三棱柱ABC-A′B′C′的底面边长为
,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C′,若侧面AA′C′C紧贴墙面(不能通行),则爬行的最短路程是( )

| 3 |

分析:由题意可知一蚂蚁从顶点A出发,沿正三棱柱的表面爬到顶点C′,那么这只蚂蚁所走过的最短路程就是,侧面展开图中AC′的距离.利用勾股定理求解即可.
解答: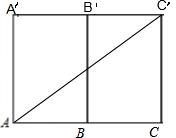 解:画出棱柱的部分侧面展开图,如图,因为正三棱柱的底面边长为
解:画出棱柱的部分侧面展开图,如图,因为正三棱柱的底面边长为
,高为2,
一蚂蚁从顶点A出发,沿正四棱柱的表面爬到顶点C′,那么这只蚂蚁所走过的最短路程为:
AC′=
=
=4.
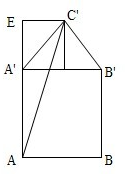 将上底面展开,则此时A'E=
将上底面展开,则此时A'E=
×
=
,C'E=
,
所以AC′=
=
=
<4,
所以最小值为
,
故选,A.
 解:画出棱柱的部分侧面展开图,如图,因为正三棱柱的底面边长为
解:画出棱柱的部分侧面展开图,如图,因为正三棱柱的底面边长为| 3 |
一蚂蚁从顶点A出发,沿正四棱柱的表面爬到顶点C′,那么这只蚂蚁所走过的最短路程为:
AC′=
| AC2+CC′2 |
(2
|
 将上底面展开,则此时A'E=
将上底面展开,则此时A'E=
| ||
| 2 |
| 3 |
| 3 |
| 2 |
| ||
| 2 |
所以AC′=
| AE2+C′E2 |
(2+
|
| 13 |
所以最小值为
| 13 |
故选,A.
点评:本题是基础题,考查棱柱的侧面展开图的应用,考查计算能力.属于基础题.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
 如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为
如图所示,已知三棱柱A′B′C′-ABC的侧棱垂直于底面,AC⊥CB,且AC=CB=CC′=2.若点E为A′B′中点,则CE与底面ABC所成角的余弦值为 ,高为2,
,高为2,



 ,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C′,若侧面AA′C′C紧贴墙面(不能通行),则爬行的最短路程是
,高为2,一只蚂蚁要从顶点A沿三棱柱的表面爬到顶点C′,若侧面AA′C′C紧贴墙面(不能通行),则爬行的最短路程是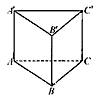


 +
+