题目内容
 如图正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为
如图正三棱柱ABC-A1B1C1中,底面边长为2,侧棱长为| 2 |
经过对角线AB1的平面交棱A1C1于点D.
(Ⅰ)试确定D点的位置使平面AB1D∥BC1,并证明你的结论;
(Ⅱ)在(Ⅰ)的条件下,求二面角A1-AB1-D的大小.
分析:(Ⅰ)由图形判断知,D为A1C1中点时平面AB1D∥BC1,证明用线面平行的判定定理即可.
(II)在图形中作出二面角的平面角,要充分利用已有的结论,作DM⊥A1B1于M,连接ME,证出角MED即平面角.
(II)在图形中作出二面角的平面角,要充分利用已有的结论,作DM⊥A1B1于M,连接ME,证出角MED即平面角.
解答:解:(Ⅰ)D为棱A1C1中点时平面AB1D∥BC1,证明如下:
连接AB1,与线AB1交于点E,
∵正三棱柱ABC-A1B1C1
∴E是中点,又D中点,
故DE是三角形A1BC1的中位线,故DE∥BC1,
又BC1不在平面AB1D内,DE在面AB1D内,
由线面平行的判定定理知平面AB1D∥BC1
(II)若D是中点,由题设条件AD=
,B1D=
,
在等腰直角三角形B1DA中,E是斜边中点,故DE⊥AB1,计算得AB1=
,故DE=
作DM⊥A1B1于M,连接ME,因为正三棱柱ABC-A1B1C1中,
所以DM⊥面AA1B1B,即DM⊥AB1,所以面DME⊥AB1,
所以∠MED即二面角的平面角,由D是中点,所以DM=
在直角三角形DME中,sin∠MED=
=
=
所以∠MED=
连接AB1,与线AB1交于点E,
∵正三棱柱ABC-A1B1C1
∴E是中点,又D中点,
故DE是三角形A1BC1的中位线,故DE∥BC1,
又BC1不在平面AB1D内,DE在面AB1D内,
由线面平行的判定定理知平面AB1D∥BC1
(II)若D是中点,由题设条件AD=
| 3 |
| 3 |
在等腰直角三角形B1DA中,E是斜边中点,故DE⊥AB1,计算得AB1=
| 6 |
| ||
| 2 |
作DM⊥A1B1于M,连接ME,因为正三棱柱ABC-A1B1C1中,
所以DM⊥面AA1B1B,即DM⊥AB1,所以面DME⊥AB1,
所以∠MED即二面角的平面角,由D是中点,所以DM=
| ||
| 2 |
在直角三角形DME中,sin∠MED=
| MD |
| DE |
| ||||
|
| ||
| 2 |
所以∠MED=
| π |
| 4 |
点评:考查正三棱柱的几何性质、线面平行的判定定理、二面角的求法,技巧性强,对空间想象力要求较高.

练习册系列答案
相关题目
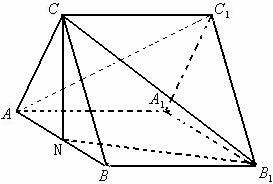 如图正三棱柱ABC-A1B1C1,
如图正三棱柱ABC-A1B1C1,
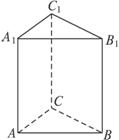 (本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.
(本题满分12分) 如图,正三棱柱ABC—A1B1C1的所有棱长均为2,P是侧棱AA1上任意一点.