题目内容
已知拋物线x2=4py(p>0)与双曲线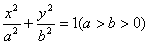 有相同的焦点F,点A 是两曲线的一个交点,且AF丄y轴,则双曲线的离心率为
有相同的焦点F,点A 是两曲线的一个交点,且AF丄y轴,则双曲线的离心率为
A,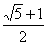 B.
B. 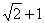 C.
C. 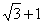 D.
D. 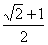
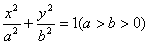 有相同的焦点F,点A 是两曲线的一个交点,且AF丄y轴,则双曲线的离心率为
有相同的焦点F,点A 是两曲线的一个交点,且AF丄y轴,则双曲线的离心率为A,
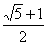 B.
B. 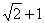 C.
C. 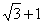 D.
D. 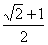
B
试题分析:根据抛物线和双曲线有相同的焦点求得p和c的关系,根据AF⊥x轴可判断出|AF|的值和A的坐标,代入双曲线方程与p=2c,b2=c2-a2联立求得a和c的关系式,然后求得离心率e.解:∵抛物线的焦点和双曲线的焦点相同,∴p=2c,∵A是它们的一个公共点,且AF垂直x轴,设A点的纵坐标大于0
∴|AF|=p,∴A(
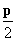 ,p)∵点A在双曲线上
,p)∵点A在双曲线上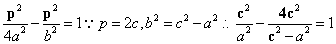 化简得:c4-6c2a2+a4=0,∴e4-6e2+1=0,∵e2>1,∴e2=3+2
化简得:c4-6c2a2+a4=0,∴e4-6e2+1=0,∵e2>1,∴e2=3+2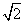 ,故有e为
,故有e为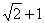 ,选B.
,选B.点评:本题主要考查关于双曲线的离心率的问题,属于中档题,本题利用焦点三角形中的边角关系,得出a、c的关系,从而求出离心率

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
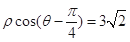 ,曲线
,曲线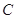 :
: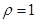 上的点到直线的距离为
上的点到直线的距离为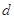 ,则
,则 ,
, 为双曲线
为双曲线 的右焦点,点
的右焦点,点 ,
, 为
为 轴正半轴上的动点。
轴正半轴上的动点。 的最大值为( )
的最大值为( )



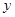 轴上,渐近线方程为
轴上,渐近线方程为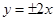 的双曲线的离心率为_______.
的双曲线的离心率为_______.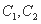 都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线
都是以原点O为对称中心、坐标轴为对称轴、离心率相等的椭圆.点M的坐标是(0,1),线段MN是曲线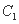 的短轴,并且是曲线
的短轴,并且是曲线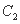 的长轴 . 直线
的长轴 . 直线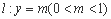 与曲线
与曲线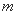 =
=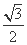 ,
,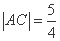 时,求椭圆
时,求椭圆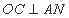 ,求
,求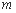 的值.
的值.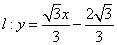 过双曲线
过双曲线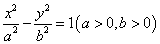 的一个焦点,且与双曲线的一条渐近线平行.
的一个焦点,且与双曲线的一条渐近线平行.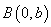 与
与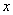 轴不平行的直线与双曲线相交于不同的两点
轴不平行的直线与双曲线相交于不同的两点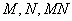 的垂直平分线为
的垂直平分线为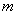 ,求直线
,求直线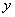 轴上截距的取值范围.
轴上截距的取值范围.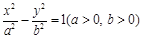 左焦点
左焦点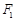 的直线与以右焦点
的直线与以右焦点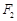 为圆心、
为圆心、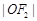 为半径的圆相切于A点,且
为半径的圆相切于A点,且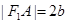 ,则双曲线的离心率为
,则双曲线的离心率为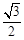

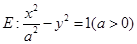 的离心率等于
的离心率等于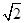 ,直线
,直线 与双曲线
与双曲线 的右支交于
的右支交于 两点.
两点.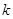 的取值范围;
的取值范围; ,点
,点 是双曲线
是双曲线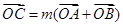 ,求
,求