题目内容
18.设数列{an}是首项为a1、公差为1的等差数列,Sn为其前n项和,若S1,S2,S4成等比数列,则a1=( )| A. | 2 | B. | $\frac{1}{2}$ | C. | -2 | D. | -$\frac{1}{2}$ |
分析 由等差数列的求和公式和等比数列可得关于a1的方程,解方程可得.
解答 解:由题意可得S22=S1•S4,
∴(2a1+1)2=a1•(4a1+6),
解得a1=$\frac{1}{2}$,
故选:B.
点评 本题考查等差数列的求和公式和等比数列,属基础题.

练习册系列答案
相关题目
13.下列式子中,错误的是( )
| A. | $(\frac{1}{x})'=-\frac{1}{x^2}$ | B. | (cos(2x+1))′=-2sin(2x+1) | ||
| C. | $(x{log_a}x)'={log_a}x+\frac{1}{lna}$ | D. | $(\frac{{e}^{x}}{x})′=\frac{{e}^{x}•x+{e}^{x}}{{x}^{2}}$ |
3.已知集合A={-1,0,1,2},集合B={x∈R|x2=1},则A∩B=( )
| A. | {1} | B. | {-1,1} | C. | {-1,0,1} | D. | {-1,0,1,2} |
7.如图所示,平面内z1,z2对应的向量分别是$\overrightarrow{OA}$,$\overrightarrow{OB}$,则|z1+z2|=( )
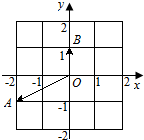

| A. | 2 | B. | 3 | C. | 2 $\sqrt{2}$ | D. | 3 $\sqrt{3}$ |
 已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.
已知函数$y=sin(ωx+φ)(ω>0,0<φ≤\frac{π}{2})$的部分图象如图所示.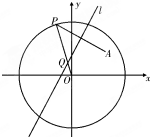 如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )
如图,已知点A为圆x2+y2=16内一定点,P是圆上任意一点,线段AP的垂直平分线l和半径OP相交于点Q,当点P在圆上运动时,点Q的轨迹是( )