Question

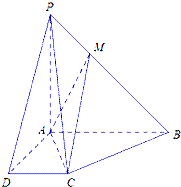
【题目】如图，在三棱台ABO﹣A1B1O1中，侧面AOO1A1与侧面OBB1O1是全等的直角梯形，且OO1⊥OB，OO1⊥OA，平面AOO1A1⊥平面OBB1O1 ， OB=3，O1B1=1，OO1= ．

（1）证明：AB1⊥BO1；
（2）求直线AO1与平面AOB1所成的角的正切值；
（3）求二面角O﹣AB1﹣O1的余弦值．

Answer 1

【答案】
（1）证明：由题设知OA⊥OO1，且平面AOO1A1⊥平面OBB1O1，

平面AOO1A1∩平面OBB1O1=OO1，

则OA⊥平面OBB1O1，所以OA⊥OB，OA⊥BO1，

又因为 ．O1B1=1，OB=3，

所以∠OO1B=60°，∠O1OB1=30°，

从而OB1⊥BO1，又因为OA⊥BO1，OB1∩OA=O，

故BO1⊥平面AOB1，又AB1平面AOB1，故AB1⊥BO1

（2）解：以O为原点，OA、OB、OO1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，

如图，则A（3，0，0），B（0，3，0），B1（0，1， ），O1（0，0， ）．

由（1）知BO1⊥平面OA B1，从而 是平面OA B1的一个法向量．

， ，

设直线AO1与平面AOB1所成的角为α，

．cosα= = ，

tanα= = ．

∴直线AO1与平面AOB1所成的角的正切值为

（3）解：由（II）知 是平面OA B1的一个法向量．且 ，

设 是平面O1A B1的一个法向量，

由 ，得 ．

设二面角O﹣AB1﹣O1的大小为，

则cosθ=cos＜， ＞=

即二面角O﹣AB1﹣O1的余弦值是

【解析】（1）推导出OA⊥OB，OA⊥BO1 ， OB1⊥BO1 ， OA⊥BO1 ， 从而BO1⊥平面AOB1 ， 由此能证明AB1⊥BO1 ． （2）以O为原点，OA、OB、OO1所在直线分别为x轴、y轴、z轴建立空间直角坐标系，利用向量法能求出直线AO1与平面AOB1所成的角的正切值．（3）求出平面OA B1的一个法向量和平面O1A B1的一个法向量，利用向量法能求出二面角O﹣AB1﹣O1的余弦值．
【考点精析】本题主要考查了空间角的异面直线所成的角的相关知识点，需要掌握已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则才能正确解答此题．