题目内容
【题目】已知存在常数![]() ,那么函数
,那么函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,再由函数的奇偶性可知在
上是增函数,再由函数的奇偶性可知在![]() 上是增函数,在
上是增函数,在![]() 上是减函数.
上是减函数.
(1)判断函数![]() 的单调性,并证明:
的单调性,并证明:
(2)将前述的函数![]() 和
和![]() 推广为更为一般形式的函数
推广为更为一般形式的函数![]() ,使
,使![]() 和
和![]() 都是
都是![]() 的特例,研究
的特例,研究![]() 的单调性(只须归纳出结论,不必推理证明)
的单调性(只须归纳出结论,不必推理证明)
【答案】![]() 见解析;
见解析;![]() 见解析.
见解析.
【解析】
![]() 采用换元的思想:令
采用换元的思想:令![]() 则
则![]() ;再借助复合函数单调性的判断规则和奇偶函数在对称区间上的单调性特点,即可得证.
;再借助复合函数单调性的判断规则和奇偶函数在对称区间上的单调性特点,即可得证.
![]() 由
由![]() 结论和题中
结论和题中![]() 的性质进行归纳总结,即可得出一般性结论.
的性质进行归纳总结,即可得出一般性结论.
![]() 判断如下:
判断如下:
![]() 在
在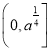 上为减函数,
上为减函数,
在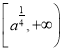 上为增函数;
上为增函数;
再由函数的奇偶性可知,
在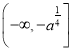 上为减函数,
上为减函数,
在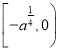 上为增函数.
上为增函数.
证明:令![]() ,
,
则![]() ,
,
由题可得,
![]() 在
在![]() 上为减函数,
上为减函数,
在![]() 上是增函数;
上是增函数;
![]() 在
在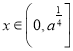 上为增函数,
上为增函数,
在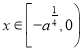 上为减函数;
上为减函数;
![]() 由复合函数单调性判断规则知:
由复合函数单调性判断规则知:
![]() 在
在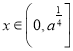 上为减函数,
上为减函数,
在 上为增函数;
上为增函数;
由题知,
![]() 为偶函数,
为偶函数,
![]() 偶函数在对称区间上单调性相反,
偶函数在对称区间上单调性相反,
![]()
![]() 在
在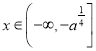 上为减函数,
上为减函数,
在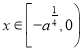 上为增函数;
上为增函数;
![]() 一般性结论:
一般性结论:
函数![]()
![]() 在
在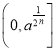 上为减函数,
上为减函数,
在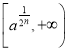 上为增函数;
上为增函数;
再由函数的奇偶性可知,
当n为奇数时,
在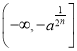 上为增函数,
上为增函数,
在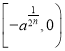 上为减函数;
上为减函数;
当n为偶数时,
在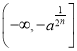 上为减函数,
上为减函数,
在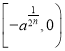 上为增函数;
上为增函数;

练习册系列答案
相关题目