题目内容
设函数 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有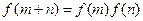 且当
且当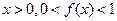
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减。
 定义在R上,对任意实数m、n,恒有
定义在R上,对任意实数m、n,恒有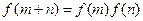 且当
且当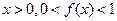
(1)求证:f(0)=1,且当x<0时,f(x)>1;
(2)求证:f(x)在R上递减。
略
(1)证明:在f(m+n)=f(m)f(n)中,
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1…………………2分
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)=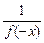 >1……………………….6分
>1……………………….6分
(2)证明:设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1………………….8分
令m=x1,m+n=x2,则n=x2-x1,代入条件式,得f(x2)=f(x1)·f(x2-x1),…10分
即0<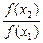 <1.∴f(x2)<f(x1)……………….12分
<1.∴f(x2)<f(x1)……………….12分
∴f(x)在R上单调递减………………….14分
令m=1,n=0,得f(1)=f(1)f(0).
∵0<f(1)<1,∴f(0)=1…………………2分
设x<0,则-x>0.令m=x,n=-x,代入条件式有f(0)=f(x)·f(-x),而f(0)=1,
∴f(x)=
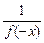 >1……………………….6分
>1……………………….6分(2)证明:设x1<x2,则x2-x1>0,∴0<f(x2-x1)<1………………….8分
令m=x1,m+n=x2,则n=x2-x1,代入条件式,得f(x2)=f(x1)·f(x2-x1),…10分
即0<
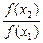 <1.∴f(x2)<f(x1)……………….12分
<1.∴f(x2)<f(x1)……………….12分∴f(x)在R上单调递减………………….14分

练习册系列答案
相关题目
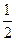 )="0," 则满足
)="0," 则满足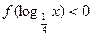 的集合为 ( )
的集合为 ( ) 10分)定义在R上的函数
10分)定义在R上的函数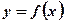 ,对任意的
,对任意的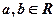 ,满足
,满足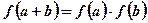 ,当
,当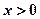 时,有
时,有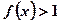 ,其中
,其中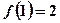 .
.
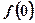 的值;
的值;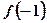 的值并判断该函数的奇偶性;
的值并判断该函数的奇偶性;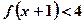 的解集.
的解集.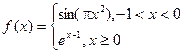 ,若
,若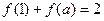 ,则
,则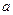 的所有可能值为___________.
的所有可能值为___________.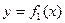 (2)
(2)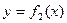 (3)
(3)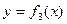 (4)
(4)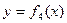 的图象如下:
的图象如下: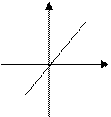
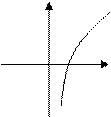
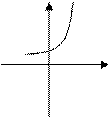
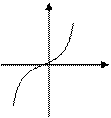
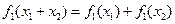
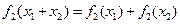

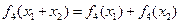
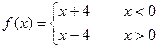 ,则
,则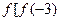 ]的值为 ( )
]的值为 ( )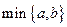 表示
表示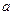 ,b两数中的最小值。若函数
,b两数中的最小值。若函数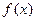 =
=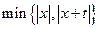 的图像关于直线
的图像关于直线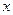 =
=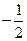 对称,则
对称,则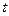 的值为
的值为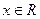 时,函数
时,函数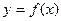 满足:
满足: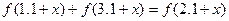 ,且
,且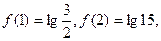 ,则
,则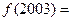 ( )
( )