题目内容
【题目】已知椭圆Γ： 
+ 
=1（a＞b＞0）的离心率与双曲线x2﹣y2=a2的离心率之和为 
，B1、B2为椭圆Γ短轴的两个端点，P是椭圆Γ上一动点（不与B1、B2重合），直线B1P、B2P分别交直线l：y=4于M、N两点，△B1B2P的面积记为S1 ， △PMN的面积记为S2 ， 且S1的最大值为4 
．
（1）求椭圆Γ的方程；
（2）若S2=λS1 ， 当λ取最小值时，求点P的坐标．
【答案】
（1）
解：双曲线的离心率为 
，∴椭圆的离心率为 
，
∴ 
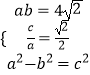，解得a=2 ，b=2，
∴椭圆方程为 
．
（2）
解：）设P（2 cosα，2sinα）（0≤α＜2π且α 
，α≠ 
），B1（0，2），B（0，﹣2），
则直线B1P的方程为y= 
x+2，直线B2P的方程为y= 
x﹣2，
∴M（ 
，4），N（ 
，4），
|MN|=| ﹣ |=| 
|，
∴S2= 
×|MN|×（4﹣2sinα）= 
，又S1= 
=4 |cosα|，
∴λ= 
= 
=（ 
）2，
令f（α）= ，则f′（α）= 
，
令f′（α）=0得α= 
或α= 
，
当0 
时，f′（α）＜0，当 
时，f′（α）＞0，当 
时，f′（α）＞0，
当 
时，f′（α）＜0，当 
时，f′（α）＜0，
∴f（α）在[0， ]上单调递减，在（ ， 
）上单调递增，在（ ， ]上单调递增，在（ ， ）上单调递减，在（ ，2π）上单调递减，
∴当 
时，f（α）取得极小值f（ ）= 
= 
，当α= 时，f（α）取得极大值f（ ）= 
=﹣ ，
∴当α= 或 时，|f（α）|取得最小值 ，
∴λ=f2（α）的最小值为 ．
∴当λ取得最小值时，P点坐标为（ 
，1）或（﹣ ，1）．
【解析】（1）根据椭圆的离心率，S1的面积列方程组，解出a，b即可得出椭圆方程；（2）设P（2 cosα，2sinα），分别求出直线方程，得出M，N的坐标，用α表示出S1 ， S2 ， 从而得到λ关于α的函数，利用导数判断此函数的单调性，得出λ的最小值及其对应的α，从而得出P点坐标．
