题目内容
下列命题:
①命题“若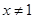 ,则
,则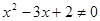 ”的逆否命题: “若
”的逆否命题: “若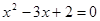 ,则
,则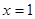 ”.
”.
②命题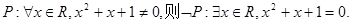
③“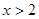 ”是“
”是“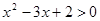 ”的充分不必要条件.
”的充分不必要条件.
④若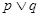 为真命题,则
为真命题,则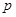 ,
,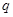 均为真命题.
均为真命题.
其中真命题的个数有
①命题“若
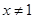 ,则
,则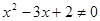 ”的逆否命题: “若
”的逆否命题: “若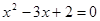 ,则
,则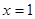 ”.
”.②命题
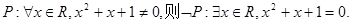
③“
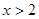 ”是“
”是“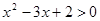 ”的充分不必要条件.
”的充分不必要条件.④若
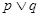 为真命题,则
为真命题,则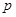 ,
,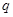 均为真命题.
均为真命题.其中真命题的个数有
| A.4个 | B.3个 |
| C.2个 | D.1个 |
B
试题分析:因为求解一个命题的逆否命题就是将原命题中的结论的否定作为条件,条件的豆丁作为结论得到的新命题即①命题“若
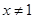 ,则
,则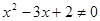 ”的逆否命题: “若
”的逆否命题: “若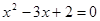 ,则
,则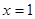 ”.成立。
”.成立。②中对于全称命题的否定,就是将任意改为存在,命题的结论改为否定,即得到命题
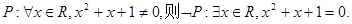 成立
成立③中条件是“
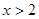 ”结论根据一元二次不等式解得为“
”结论根据一元二次不等式解得为“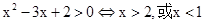 ”利用集合的思想可知小集合是大集合的充分不必要条件,故成立。.
”利用集合的思想可知小集合是大集合的充分不必要条件,故成立。.④中或命题为真,说明p,q至少有一个为真,那么题目中都是为真,因此是错误。因此可知真命题的个数为3个,选B.
点评:解决该试题的关键是对于命题中逻辑联结词概念的理解,以及命题的否定的运用。

练习册系列答案
相关题目
 ,则
,则 (
(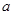 、
、 、
、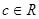 )”与它的逆命题、否命题、逆否命题中,真命题的个数为( )
)”与它的逆命题、否命题、逆否命题中,真命题的个数为( ) 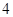
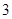


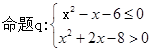
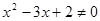 ,则
,则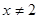 ”的逆否命题为_________
”的逆否命题为_________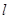 为一条直线,
为一条直线,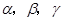 为三个互不重合的平面,给出下面三个命题:
为三个互不重合的平面,给出下面三个命题: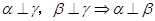 ;②
;②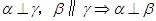 ;③
;③ .其中正确的命题有( )
.其中正确的命题有( )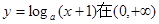 内单调递减;命题Q:曲线
内单调递减;命题Q:曲线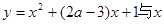 轴交于不同的两点.
轴交于不同的两点.  ,则
,则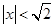 ”的逆否命题是 .
”的逆否命题是 .