题目内容
 (2004•朝阳区一模)如图,已知PA垂直于正方形ABCD所在的平面,E、F分别为AB、PD的中点,过AE、AF的平面交PC于点H,二面角P-CD-B为45°,PA=a.
(2004•朝阳区一模)如图,已知PA垂直于正方形ABCD所在的平面,E、F分别为AB、PD的中点,过AE、AF的平面交PC于点H,二面角P-CD-B为45°,PA=a.(Ⅰ)求证:AF∥EH;
(Ⅱ)求证:平面PCE⊥平面PCD;
(Ⅲ)求多面体ECDAHF的体积.
分析:(Ⅰ)利用线面平行的判定,证明EA∥平面PCD,再证明四边形EAFH是平行四边形,即可证明AF∥EH;
(Ⅱ)证明AF⊥平面PCD,可得EH⊥平面PCD,利用面面垂直的判定,可以证明平面PCE⊥平面PCD;
(Ⅲ)利用V多面体ECDAHF=VP-AECD-VP-EAFH,可求多面体ECDAHF的体积.
(Ⅱ)证明AF⊥平面PCD,可得EH⊥平面PCD,利用面面垂直的判定,可以证明平面PCE⊥平面PCD;
(Ⅲ)利用V多面体ECDAHF=VP-AECD-VP-EAFH,可求多面体ECDAHF的体积.
解答:(Ⅰ)证明:∵EA∥CD,CD?平面PCD,EA?平面PCD,
∴EA∥平面PCD.
又平面EAFH∩平面PCD=HF,且EA?平面EAFH,
∴EA∥HF.
∴HF∥CD.
∵E、F分别是AB、PD的中点,
∴EA∥HF∥CD,EA=HF=
CD.
∴四边形EAFH是平行四边形.
∴AF∥EH.…(5分)
(Ⅱ)证明:∵PA⊥平面ABCD,AD⊥CD,AD是PD在平面ABCD内的射影,
∴PD⊥CD.
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°.
∴△PAD是等腰Rt△,又F是斜边PD上的中点,
∴AF⊥PD.
∵AF在平面ABCD内的射影AD⊥CD,
∴AF⊥CD,而PD∩CD=D.
∴AF⊥平面PCD.
∵EH∥AF,∴EH⊥平面PCD.
又EH?平面PCE,∴平面PCE上平面PCD.…(9分)
(Ⅲ)解:由上面的证明可知,PF⊥平面EAFH,四边形EAFH是矩形,
∵PA=AD=a,
∴AF=PF=
a,HF=
.
∴VP-EAFH=
AF•HF•PF=
•
a•
•
a=
.
=
(
+a)•a•a=
∴V多面体ECDAHF=VP-AECD-VP-EAFH=
-
=
.…(13分)
∴EA∥平面PCD.
又平面EAFH∩平面PCD=HF,且EA?平面EAFH,
∴EA∥HF.
∴HF∥CD.
∵E、F分别是AB、PD的中点,
∴EA∥HF∥CD,EA=HF=
| 1 |
| 2 |
∴四边形EAFH是平行四边形.
∴AF∥EH.…(5分)
(Ⅱ)证明:∵PA⊥平面ABCD,AD⊥CD,AD是PD在平面ABCD内的射影,
∴PD⊥CD.
∴∠PDA是二面角P-CD-B的平面角,即∠PDA=45°.
∴△PAD是等腰Rt△,又F是斜边PD上的中点,
∴AF⊥PD.
∵AF在平面ABCD内的射影AD⊥CD,
∴AF⊥CD,而PD∩CD=D.
∴AF⊥平面PCD.
∵EH∥AF,∴EH⊥平面PCD.
又EH?平面PCE,∴平面PCE上平面PCD.…(9分)
(Ⅲ)解:由上面的证明可知,PF⊥平面EAFH,四边形EAFH是矩形,
∵PA=AD=a,
∴AF=PF=
| ||
| 2 |
| a |
| 2 |
∴VP-EAFH=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
| a |
| 2 |
| ||
| 2 |
| a3 |
| 12 |
|
| 1 |
| 6 |
| a |
| 2 |
| a3 |
| 4 |
∴V多面体ECDAHF=VP-AECD-VP-EAFH=
| a3 |
| 4 |
| a3 |
| 12 |
| a3 |
| 6 |
点评:本题考查线面平行的判定与性质,考查面面垂直,考查多面体体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
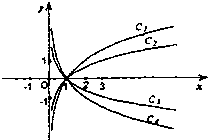 (2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )
(2004•朝阳区一模)已知图中曲线C1、C2、C3、C4是函数logax的图象,则曲线C1、C2、C3、C4对应的a的值依次为( )