Question

【题目】某校同时提供、两类线上选修课程，类选修课每次观看线上直播分钟，并完成课后作业分钟，可获得积分分；类选修课每次观看线上直播分钟，并完成课后作业分钟，可获得积分分．每周开设次，共开设周，每次均为独立内容，每次只能选择类、类课程中的一类学习．当选择类课程次，类课程次时，可获得总积分共_______分．如果规定学生观看直播总时间不得少于分钟，课后作业总时间不得少于分钟，则通过线上选修课的学习，最多可以获得总积分共________分．

Answer 1

【答案】

【解析】

根据题意可计算出当选择类课程次，类课程次时，可获得的总积分；设学生选择类选修课次，类选修课次，根据题意列出有关、的约束条件，可得出目标函数为，利用线性规划思想可求得的最大值，进而得解.

根据题意，当选择类课程次，类课程次时，可获得总积分分.

设学生选择类选修课次，类选修课次，

则、所满足的约束条件为，即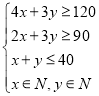，目标函数为，如下图所示：

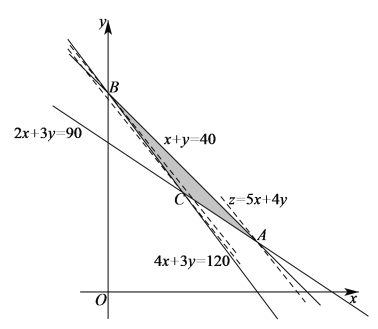
则可行域为图中阴影部分中的整数点（横坐标和纵坐标均为整数的点），

联立，解得，可得点，

平移直线，当直线经过可行域的顶点时，直线在轴上的截距最大，此时取最大值，即.

因此，通过线上选修课的学习，最多可以获得总积分共分.

故答案为：；.