题目内容
已知 ,则
,则 __ ___.
__ ___.
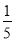
【解析】
试题分析:由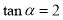 利用直角三角形,把
利用直角三角形,把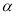 看做锐角对边为
看做锐角对边为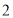 邻边为
邻边为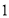 则斜边为
则斜边为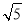 ,可得
,可得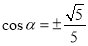 ,
,
从而的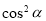 .
.
考点:同角三角函数关系

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
题目内容
已知 ,则
,则 __ ___.
__ ___.
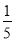
【解析】
试题分析:由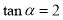 利用直角三角形,把
利用直角三角形,把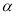 看做锐角对边为
看做锐角对边为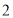 邻边为
邻边为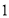 则斜边为
则斜边为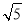 ,可得
,可得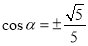 ,
,
从而的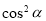 .
.
考点:同角三角函数关系

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案