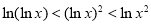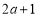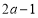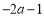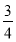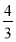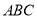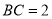题目内容
已知函数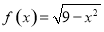 的定义域为集合
的定义域为集合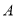 .
.
(1)若函数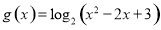 的定义域也为集合
的定义域也为集合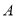 ,
,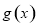 的值域为
的值域为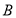 ,求
,求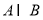 ;
;
(2)已知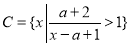 ,若
,若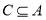 ,求实数
,求实数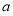 的取值范围.
的取值范围.
(1)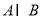
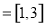 ;(2)
;(2)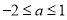 .
.
【解析】
试题分析:(1)对数定义域真数大于零求定义域,有真数范围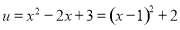 ,
,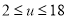 求值域;(2解不等式
求值域;(2解不等式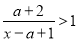 (注意移项通分)化分式不等式为整式不等式
(注意移项通分)化分式不等式为整式不等式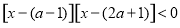 ,
,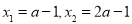 ,对
,对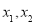 大小关系分三类讨论,再分别求满足
大小关系分三类讨论,再分别求满足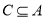 的值.
的值.
试题解析:(1)由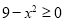 ,得
,得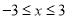 ,
,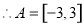 , 2分
, 2分
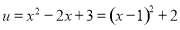 , 3分
, 3分
当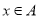 时,
时,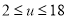 ,于是
,于是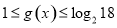 ,即
,即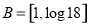 , 5分
, 5分
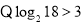 ,
,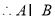
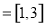 。 7分
。 7分
(2))由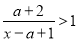 ,得
,得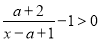 ,即
,即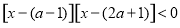 . .8分
. .8分
当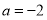 时,
时,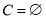 ,满足
,满足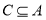 ; 9分
; 9分
当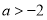 时,
时,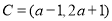 ,
,
因为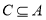 ,所以
,所以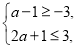 解得
解得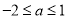 , 11分
, 11分
又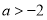 ,所以
,所以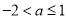 ;
;
当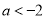 时,
时,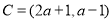 ,
,
因为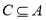 ,所以
,所以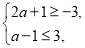 解得
解得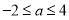 ,
,
又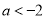 ,所以此时无解; 13分
,所以此时无解; 13分
综上所述,实数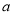 的取值范围是
的取值范围是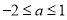 . 14分
. 14分
考点:1.函数定义域值域;2.分类讨论思想;3.集合运算.

练习册系列答案
相关题目