题目内容
【题目】已知曲线
的参数方程为
（
为参数），以坐标原点
为极点，
轴的正半轴为极轴建立极坐标系，曲线
的极坐标方程为
.
（1）写出曲线的极坐标方程，并求出曲线与公共弦所在直线的极坐标方程；
（2）若射线
与曲线交于
两点，与曲线交于
点，且
，求
的值.
【答案】（1）曲线
的极坐标方程为
，公共弦所在直线的极坐标方程
（2）
【解析】
（1）先得到C1的一般方程，再由极坐标与直角坐标的互化公式得到极坐标方程，将
，联立，得到公共弦所在直线的极坐标方程；
（2）先求得|OA|，|OB|，可得
|OA|
|OB|，化简可得到
.
（1）曲线的直角坐标方程为
，将极坐标与直角坐标的互化公式：
代入，
可得曲线的极坐标方程为.
联立与，得
∴曲线与
公共弦所在直线的极坐标方程,（或
和
）
（2）把
，代入，，
得
；
又，则
=2，可得
所以，
【题目】自从新型冠状病毒爆发以来，全国范围内采取了积极的措施进行防控，并及时通报各项数据以便公众了解情况，做好防护.以下是湖南省2020年1月23日-31日这9天的新增确诊人数.
日期 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 |
时间 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
新增确诊人数 | 15 | 19 | 26 | 31 | 43 | 78 | 56 | 55 | 57 |
经过医学研究，发现新型冠状病毒极易传染，一个病毒的携带者在病情发作之前通常有长达14天的潜伏期，这个期间如果不采取防护措施，则感染者与一位健康者接触时间超过15秒，就有可能传染病毒.
（1）将1月23日作为第1天，连续9天的时间作为变量x，每天新增确诊人数作为变量y，通过回归分析，得到模型
用于对疫情进行分析.对上表的数据作初步处理，得到下面的一些统计量的值（部分数据已作近似处理）：
，
.根据相关数据，求该模型的回归方程（结果精确到0.1），并依据该模型预测第10天新增确诊人数.
（2）如果一位新型冠状病毒的感染者传染给他人的概率为0.3，在一次12人的家庭聚餐中，只有一位感染者参加了聚餐，记余下的人员中被感染的人数为
，求
最有可能（即概率最大）的值是多少.
附：对于一组数据
，
…，
，其回归直线
的斜率和截距的最小二乘估计分别为
.
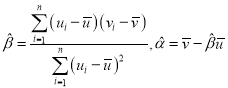【题目】
甲、乙两个篮球运动员互不影响地在同一位置投球，命中率分别为
与
，且乙投球2次均未命中的概率为
.
（Ⅰ）求乙投球的命中率；
（Ⅱ）若甲投球1次，乙投球2次，两人共命中的次数记为
，求的分布列和数学期望.
