题目内容
 选修4-1:几何证明选讲
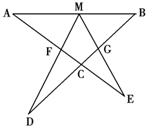
选修4-1:几何证明选讲如图设M为线段AB中点,AE与BD交于点C∠DME=∠A=∠B=α,且DM交AC于F,EM交BD于G.
(1)写出图中三对相似三角形,并对其中一对作出证明;
(2)连接FG,设α=45°,AB=4
| 2 |
分析:(1)根据已知条件,∠DME=∠A=∠B=α,结合图形上的公共角,即可推出△DMG∽△DBM,△EMF∽△EAM,AMF∽△BGM;
(2)根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
(2)根据相似三角形的性质,推出BG的长度,依据锐角三角函数推出AC的长度,即可求出CG、CF的长度,继而推出FG的长度.
解答:解:(1)△AME∽△MFE,△BMD∽△MGD,△AMF∽△BGM,…(3分)
∵∠AMD=∠B+∠D,∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=α
∴∠AMF=∠BGM,
∴△AMF∽△BGM,…(5分)
(2)连接FG,
由(1)知,△AMF∽△BGM,
=
,BG=
∠α=45°,
∴△ABC为等腰直角三角形,
AB=4
,AC=BC=4,CF=AC-AF=1,
CG=4-
=
,
∴由勾股定理得FG=
.…(10分)
∵∠AMD=∠B+∠D,∠BGM=∠DMG+∠D
又∠B=∠A=∠DME=α
∴∠AMF=∠BGM,
∴△AMF∽△BGM,…(5分)
(2)连接FG,
由(1)知,△AMF∽△BGM,
| BG |
| AM |
| BM |
| AF |
| 8 |
| 3 |
∠α=45°,
∴△ABC为等腰直角三角形,
AB=4
| 2 |
CG=4-
| 8 |
| 3 |
| 4 |
| 3 |
∴由勾股定理得FG=
| 5 |
| 3 |
点评:本题主要考查相似三角形的判定和性质、解直角三角形、等腰三角形的性质,解题的关键找到相似的三角形,根据其性质求出BG、AC的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 A、选修4-1:几何证明选讲
A、选修4-1:几何证明选讲  选修4-1:几何证明选讲
选修4-1:几何证明选讲 (2012•徐州模拟)选修4-1:几何证明选讲
(2012•徐州模拟)选修4-1:几何证明选讲 (2013•南京二模)选修4-1:几何证明选讲
(2013•南京二模)选修4-1:几何证明选讲