��Ŀ����
����Ŀ��ij�༶��ĩ���Ժ���ѧ�ɼ���![]() �����ϣ���
�����ϣ���![]() �֣���ѧ���ɼ�����ͳ�ƣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.����
�֣���ѧ���ɼ�����ͳ�ƣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ.����![]() �����ε�����Ϊ
�����ε�����Ϊ![]() ��.
��.
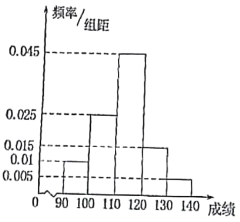
��1������Ƶ�ʷֲ�ֱ��ͼ��д���ð༶ѧ����ѧ�ɼ���������
��2���ָ���ѧ����ѧ�ɼ��ӵ�һ��͵����飨�ӵͷֶε��߷ֶ�����Ϊ��һ�飬�ڶ��飬![]() �������飩������ѡ�������γ�ѧϰС��.��ѡ�������˳ɼ�֮�����
�������飩������ѡ�������γ�ѧϰС��.��ѡ�������˳ɼ�֮�����![]() �����������Ϊ�������ϡ�������ѡ��������Ϊ�������ϡ��ĸ���.
�����������Ϊ�������ϡ�������ѡ��������Ϊ�������ϡ��ĸ���.
���𰸡���1������Ϊ![]() ����2��
����2��![]() .
.
��������
��1��������߾��εױߵ��е�ֵΪ�����ɵó��𰸣�
��2���ȼ������һ�������Ϊ![]() ���ֱ��Ϊ
���ֱ��Ϊ![]() ��
��![]() �������������Ϊ
�������������Ϊ![]() ���ֱ��Ϊ
���ֱ��Ϊ![]() ��
��![]() ��
��![]() ���оٳ����еĻ����¼������¼�
���оٳ����еĻ����¼������¼�![]() ѡ��������Ϊ�������ϡ���ȷ���¼�
ѡ��������Ϊ�������ϡ���ȷ���¼�![]() �������Ļ����¼������ùŵ���͵ĸ��ʹ�ʽ�ɼ���������¼��ĸ���.
�������Ļ����¼������ùŵ���͵ĸ��ʹ�ʽ�ɼ���������¼��ĸ���.
��1����Ƶ�ʷֲ�ֱ��ͼ��֪���ð༶ѧ����ѧ�ɼ�������Ϊ![]() ��
��
��2����һ�������Ϊ![]() ���ֱ��Ϊ
���ֱ��Ϊ![]() ��
��![]() ��
��
�����������Ϊ![]() ���ֱ��Ϊ
���ֱ��Ϊ![]() ��
��![]() ��
��![]() ��
��
�ڵ�һ��͵�����������ѡ�������γ�ѧϰС�飬���еĻ����¼��У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �֣�
�֣�
���¼�![]() ѡ��������Ϊ�������ϡ�������ѡ�����˱��������Բ�ͬ�����飬
ѡ��������Ϊ�������ϡ�������ѡ�����˱��������Բ�ͬ�����飬
�¼�![]() �������Ļ����¼��У�
�������Ļ����¼��У�![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �֣�
�֣�
��ˣ�![]() .
.

 �ִʾ�ƪ��ͬ�����Ĵ��ϵ�д�
�ִʾ�ƪ��ͬ�����Ĵ��ϵ�д� �߽�������ϵ�д�
�߽�������ϵ�д�