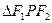题目内容
(本小题满分14分)
设椭圆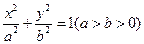 的左、右焦点分别为
的左、右焦点分别为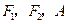 是椭圆上的一点,
是椭圆上的一点,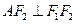 ,原点
,原点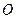 到直线
到直线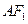 的距离为
的距离为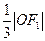 .
.
(Ⅰ)证明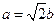 ;
;
(Ⅱ)设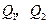 为椭圆上的两个动点,
为椭圆上的两个动点,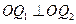 ,过原点
,过原点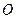 作直线
作直线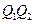 的垂线
的垂线 ,垂足为
,垂足为 ,求点
,求点 的轨迹方程.
的轨迹方程.
设椭圆
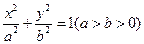 的左、右焦点分别为
的左、右焦点分别为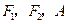 是椭圆上的一点,
是椭圆上的一点,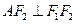 ,原点
,原点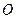 到直线
到直线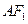 的距离为
的距离为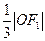 .
.(Ⅰ)证明
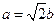 ;
;(Ⅱ)设
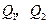 为椭圆上的两个动点,
为椭圆上的两个动点,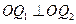 ,过原点
,过原点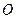 作直线
作直线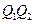 的垂线
的垂线 ,垂足为
,垂足为 ,求点
,求点 的轨迹方程.
的轨迹方程.(Ⅰ)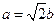
(Ⅱ)点 的轨迹方程为
的轨迹方程为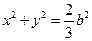
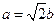
(Ⅱ)点
 的轨迹方程为
的轨迹方程为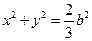
(Ⅰ)证法一:由题设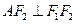 及
及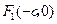 ,
,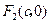 ,不妨设点
,不妨设点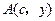 ,其中
,其中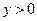 .由于点
.由于点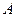 在椭圆上,有
在椭圆上,有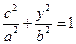 ,即
,即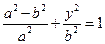 .
.
解得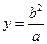 ,从而得到
,从而得到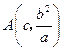 .
.
直线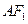 的方程为
的方程为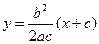 ,整理得
,整理得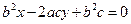 .
.
由题设,原点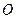 到直线
到直线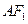 的距离为
的距离为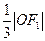 ,即
,即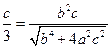 ,
,
将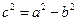 代入上式并化简得
代入上式并化简得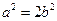 ,即
,即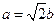 .
.
证法二:同证法一,得到点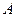 的坐标为
的坐标为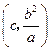 .
.
过点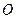 作
作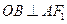 ,垂足为
,垂足为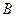 ,易知
,易知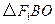
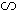
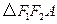 ,故
,故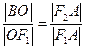 .
.
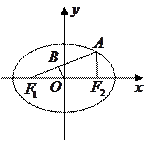 由椭圆定义得
由椭圆定义得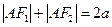 ,又
,又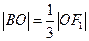 ,
,
所以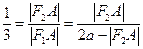 ,
,
解得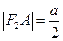 ,而
,而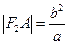 ,得
,得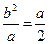 ,即
,即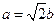 .
.
(Ⅱ)解法一:设点 的坐标为
的坐标为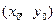 .
.
当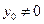 时,由
时,由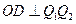 知,直线
知,直线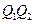 的斜率为
的斜率为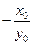 ,所以直线
,所以直线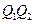 的方程为
的方程为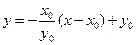 ,或
,或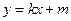 ,其中
,其中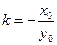 ,
,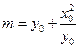 .
.
点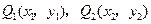 的坐标满足方程组
的坐标满足方程组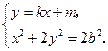
将①式代入②式,得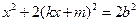 ,
,
整理得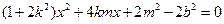 ,
,
于是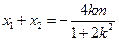 ,
,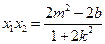 .
.
由①式得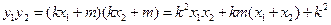
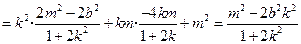 .
.
由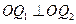 知
知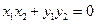 .将③式和④式代入得
.将③式和④式代入得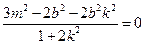 ,
,
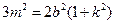 .
.
将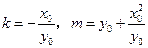 代入上式,整理得
代入上式,整理得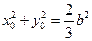 .
.
当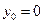 时,直线
时,直线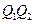 的方程为
的方程为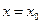 ,
,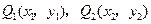 的坐标满足方程组
的坐标满足方程组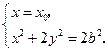
所以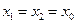 ,
,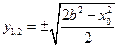 .
.
由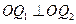 知
知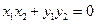 ,即
,即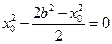 ,
,
解得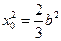 .
.
这时,点 的坐标仍满足
的坐标仍满足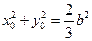 .
.
综上,点 的轨迹方程为
的轨迹方程为 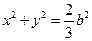 .
.
解法二:设点 的坐标为
的坐标为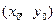 ,直线
,直线 的方程为
的方程为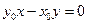 ,由
,由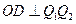 ,垂足为
,垂足为 ,可知直线
,可知直线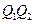 的方程为
的方程为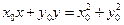 .
.
记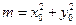 (显然
(显然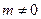 ),点
),点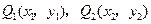 的坐标满足方程组
的坐标满足方程组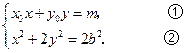
由①式得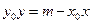 . ③
. ③
由②式得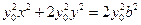 . ④
. ④
将③式代入④式得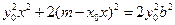 .
.
整理得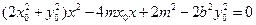 ,
,
于是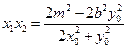 . ⑤
. ⑤
由①式得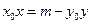 . ⑥
. ⑥
由②式得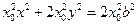 . ⑦
. ⑦
将⑥式代入⑦式得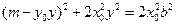 ,
,
整理得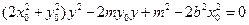 ,
,
于是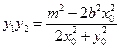 . ⑧
. ⑧
由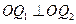 知
知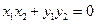 .将⑤式和⑧式代入得
.将⑤式和⑧式代入得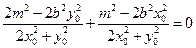 ,
,
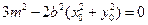 .
.
将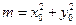 代入上式,得
代入上式,得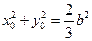 .
.
所以,点 的轨迹方程为
的轨迹方程为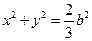 .
.
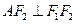 及
及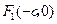 ,
,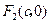 ,不妨设点
,不妨设点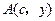 ,其中
,其中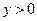 .由于点
.由于点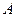 在椭圆上,有
在椭圆上,有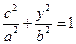 ,即
,即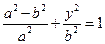 .
.解得
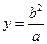 ,从而得到
,从而得到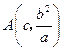 .
.直线
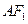 的方程为
的方程为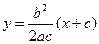 ,整理得
,整理得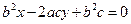 .
.由题设,原点
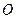 到直线
到直线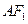 的距离为
的距离为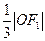 ,即
,即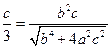 ,
,将
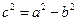 代入上式并化简得
代入上式并化简得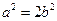 ,即
,即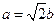 .
.证法二:同证法一,得到点
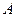 的坐标为
的坐标为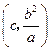 .
.过点
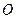 作
作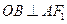 ,垂足为
,垂足为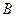 ,易知
,易知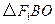
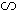
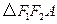 ,故
,故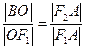 .
.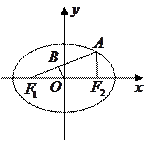 由椭圆定义得
由椭圆定义得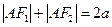 ,又
,又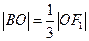 ,
,所以
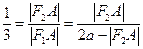 ,
,解得
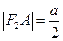 ,而
,而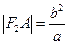 ,得
,得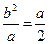 ,即
,即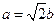 .
.(Ⅱ)解法一:设点
 的坐标为
的坐标为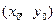 .
.当
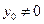 时,由
时,由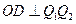 知,直线
知,直线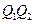 的斜率为
的斜率为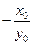 ,所以直线
,所以直线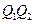 的方程为
的方程为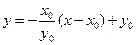 ,或
,或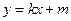 ,其中
,其中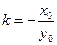 ,
,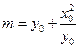 .
.点
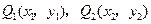 的坐标满足方程组
的坐标满足方程组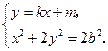
将①式代入②式,得
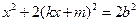 ,
,整理得
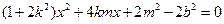 ,
,于是
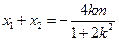 ,
,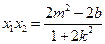 .
.由①式得
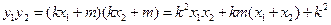
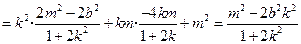 .
.由
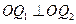 知
知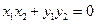 .将③式和④式代入得
.将③式和④式代入得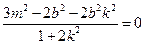 ,
,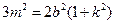 .
.将
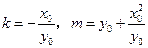 代入上式,整理得
代入上式,整理得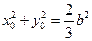 .
.当
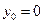 时,直线
时,直线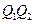 的方程为
的方程为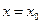 ,
,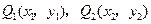 的坐标满足方程组
的坐标满足方程组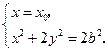
所以
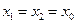 ,
,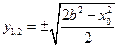 .
.由
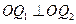 知
知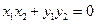 ,即
,即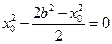 ,
,解得
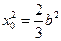 .
.这时,点
 的坐标仍满足
的坐标仍满足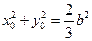 .
.综上,点
 的轨迹方程为
的轨迹方程为 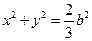 .
.解法二:设点
 的坐标为
的坐标为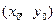 ,直线
,直线 的方程为
的方程为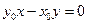 ,由
,由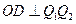 ,垂足为
,垂足为 ,可知直线
,可知直线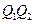 的方程为
的方程为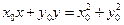 .
.记
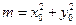 (显然
(显然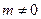 ),点
),点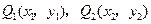 的坐标满足方程组
的坐标满足方程组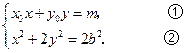
由①式得
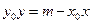 . ③
. ③由②式得
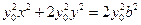 . ④
. ④将③式代入④式得
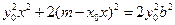 .
.整理得
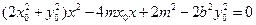 ,
,于是
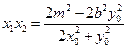 . ⑤
. ⑤由①式得
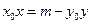 . ⑥
. ⑥由②式得
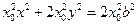 . ⑦
. ⑦将⑥式代入⑦式得
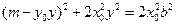 ,
,整理得
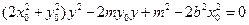 ,
,于是
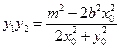 . ⑧
. ⑧由
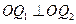 知
知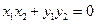 .将⑤式和⑧式代入得
.将⑤式和⑧式代入得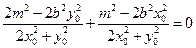 ,
,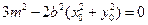 .
.将
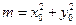 代入上式,得
代入上式,得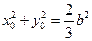 .
.所以,点
 的轨迹方程为
的轨迹方程为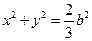 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
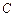 :
: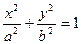 (a>b>0)的中心在原点,焦点在
(a>b>0)的中心在原点,焦点在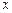 轴上,离心率为
轴上,离心率为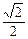 ,点F1、F2分别是椭圆的左、右焦点,在直线x=2上的点P(2,
,点F1、F2分别是椭圆的左、右焦点,在直线x=2上的点P(2, 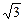 )满足|PF2|=|F1F2|,直线l:y=kx+m与椭圆C交于不同的两点A、 B.
)满足|PF2|=|F1F2|,直线l:y=kx+m与椭圆C交于不同的两点A、 B.
 存在点Q,满足
存在点Q,满足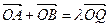 (O为坐标原点),求实数l的取值范围.
(O为坐标原点),求实数l的取值范围.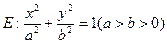 的左、右焦点分别为
的左、右焦点分别为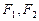 ,点
,点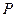 是
是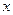 轴上方椭圆
轴上方椭圆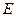 上的一点,且
上的一点,且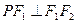 ,
, 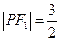 ,
, 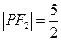 .
.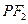 为直径的圆与以椭圆
为直径的圆与以椭圆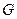 是椭圆
是椭圆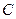 :
: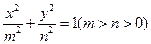 上的任意一点,
上的任意一点,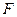 是椭圆
是椭圆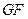 为直径的圆与以椭圆
为直径的圆与以椭圆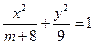 的离心率是
的离心率是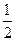 ,求椭圆两准线间的距离。
,求椭圆两准线间的距离。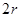 ,短半轴长为
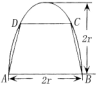
,短半轴长为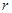 ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底 是半椭圆的短轴,上底
是半椭圆的短轴,上底 的端点在椭圆上,记
的端点在椭圆上,记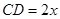 ,梯形面积为
,梯形面积为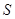 .
.
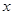 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;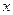 轴上,经过点
轴上,经过点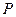
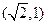 且离心率
且离心率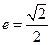 .过定点
.过定点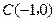 的直线与椭圆相交于
的直线与椭圆相交于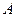 ,
,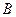 两点.
两点.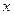 轴上是否存在点
轴上是否存在点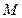 ,使
,使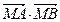 为常数?若存在,求出点
为常数?若存在,求出点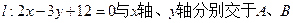 两点,则以A为焦点,经过B点的椭圆的标准方程是 .
两点,则以A为焦点,经过B点的椭圆的标准方程是 .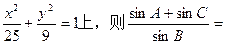 _____________________.
_____________________. 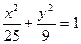 的焦点F1 、F2,P为椭圆上的一点,已知
的焦点F1 、F2,P为椭圆上的一点,已知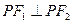 ,则
,则