题目内容
定义在R上的函数f(x)关于直线x=1对称,且对任意实数x满足f(x+1)=f(x-1),且当x∈[3,4]时,f(x)=x-2,则
- A.
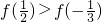
- B.
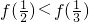
- C.
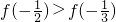
- D.
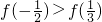
B
分析:先求出函数的周期,然后根据函数f(x)关于直线x=1对称则f(x)=f(2-x),利用性质将 、
、 、
、 、-
、- 化到区间[3,4],代入f(x)=x-2求出函数值,从而得到函数值的大小关系.
化到区间[3,4],代入f(x)=x-2求出函数值,从而得到函数值的大小关系.
解答:∵对任意实数x满足f(x+1)=f(x-1),
∴f(x+2)=f(x)则函数的周期为2
∵函数f(x)关于直线x=1对称
∴f(x)=f(2-x)
∵当x∈[3,4]时,f(x)=x-2,
∴f( )=f(2-
)=f(2- )=f(
)=f( +2)=
+2)= =
=
f(- )=f(-
)=f(- +4)=
+4)= -2=
-2=
f(- )=f(
)=f( +4)=
+4)= -2=
-2=
f( )=f(2-
)=f(2- )=f(
)=f( +2)=
+2)=
故选B
点评:本题主要考查了函数周期性以及奇偶性与单调性的综合,同时考查了转化能力,属于中档题.
分析:先求出函数的周期,然后根据函数f(x)关于直线x=1对称则f(x)=f(2-x),利用性质将
 、
、 、
、 、-
、- 化到区间[3,4],代入f(x)=x-2求出函数值,从而得到函数值的大小关系.
化到区间[3,4],代入f(x)=x-2求出函数值,从而得到函数值的大小关系.解答:∵对任意实数x满足f(x+1)=f(x-1),
∴f(x+2)=f(x)则函数的周期为2
∵函数f(x)关于直线x=1对称
∴f(x)=f(2-x)
∵当x∈[3,4]时,f(x)=x-2,
∴f(
 )=f(2-
)=f(2- )=f(
)=f( +2)=
+2)= =
=
f(-
 )=f(-
)=f(- +4)=
+4)= -2=
-2=
f(-
 )=f(
)=f( +4)=
+4)= -2=
-2=
f(
 )=f(2-
)=f(2- )=f(
)=f( +2)=
+2)=
故选B
点评:本题主要考查了函数周期性以及奇偶性与单调性的综合,同时考查了转化能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目