题目内容
过点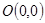 的圆C与直线
的圆C与直线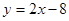 相切于点
相切于点 .
.
(1)求圆C的方程;
(2)已知点 的坐标为
的坐标为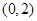 ,设
,设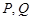 分别是直线
分别是直线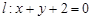 和圆
和圆 上的动点,求
上的动点,求 的最小值.
的最小值.
(3)在圆C上是否存在两点 关于直线
关于直线 对称,且以
对称,且以 为直径的圆经过原点?若存在,写出直线
为直径的圆经过原点?若存在,写出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(1)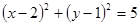
(2)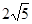
(3)直线 为
为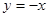 或
或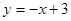
解析试题分析:解. (1)由已知得圆心经过点 ,且与
,且与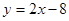 垂直的直线
垂直的直线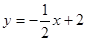 上,它又在线段OP的中垂线
上,它又在线段OP的中垂线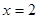 上,所以求得圆心
上,所以求得圆心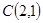 ,半径为
,半径为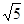 ,
,
所以圆C的方程为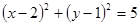 4分
4分
(2)求得点
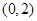 关于直线
关于直线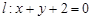 的对称点
的对称点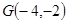 ,
,
所以
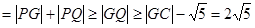 ,所以
,所以 的最小值是
的最小值是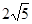 。 9分
。 9分
(3)假设存在两点 关于直线
关于直线 对称,则
对称,则 通过圆心
通过圆心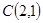 ,求得
,求得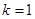 ,所以设直线
,所以设直线 为
为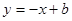 ,代入圆的方程得
,代入圆的方程得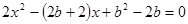 ,
,
设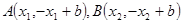 ,又
,又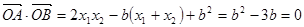 ,
,
解得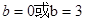 ,这时
,这时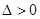 ,符合,所以存在直线
,符合,所以存在直线 为
为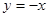 或
或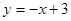 符合条件。 14分
符合条件。 14分
考点:直线与圆
点评:主要是考查了直线与圆的位置关系以及直线的对称性的运用,属于中档题。

练习册系列答案
相关题目
 ,点
,点 .
.
 上,经过点
上,经过点 ,且与圆
,且与圆 相外切的圆
相外切的圆 的方程;
的方程; 与圆
与圆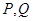 两点,且圆弧
两点,且圆弧 恰为圆
恰为圆 ,求直线
,求直线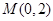 ,
, ,直线
,直线 (
( 为常数).
为常数).  、
、 到直线
到直线 的距离相等,求实数
的距离相等,求实数 ,
,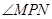 恒为锐角,求实数
恒为锐角,求实数 .请将n表示为m的函数.
.请将n表示为m的函数. ,直线
,直线 经过点
经过点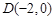 ,
, ,
, 两点,且
两点,且 为等腰直角三角形,求直线
为等腰直角三角形,求直线 的方程.
的方程.  与圆C相切.
与圆C相切. 与圆C交于不同的两点A
与圆C交于不同的两点A 、B
、B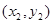 ,当
,当 时,求△AOB的面积.
时,求△AOB的面积. 的极坐标方程是
的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为
,以极点为平面直角坐标系的原点,极轴为 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线 的参数方程为
的参数方程为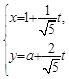 (
( 为参数).若直线
为参数).若直线 ,
, 两点,且
两点,且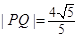 .
. 的值.
的值. 内有一点P(2,2),过点P作直线
内有一点P(2,2),过点P作直线 交圆C于A、B两点。
交圆C于A、B两点。 时,写出直线
时,写出直线 |PD|.
|PD|.