题目内容
(本小题满分12分)

过抛物线焦点垂直于对称轴的弦叫做抛物线的通径。如图,已知抛物线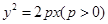 ,过其焦点F的直线交抛物线于
,过其焦点F的直线交抛物线于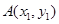 、
、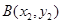 两点。过
两点。过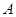 、
、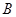 作准线的垂线,垂足分别为
作准线的垂线,垂足分别为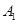 、
、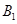 .
.
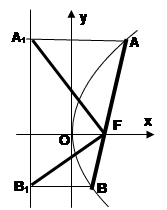
(1)求出抛物线的通径,证明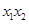 和
和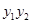 都是定值,并求出这个定值;
都是定值,并求出这个定值;
(2)证明: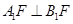 .
.

过抛物线焦点垂直于对称轴的弦叫做抛物线的通径。如图,已知抛物线
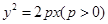 ,过其焦点F的直线交抛物线于
,过其焦点F的直线交抛物线于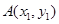 、
、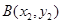 两点。过
两点。过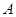 、
、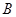 作准线的垂线,垂足分别为
作准线的垂线,垂足分别为 、
、 .
.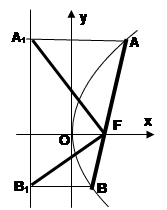
(1)求出抛物线的通径,证明
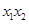 和
和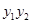 都是定值,并求出这个定值;
都是定值,并求出这个定值;(2)证明:
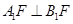 .
.(1)通径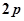 ,证明:
,证明: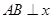 时
时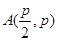 、
、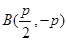 ,
,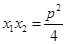 、
、 ,是定值;AB与x轴不垂直时,设AB:
,是定值;AB与x轴不垂直时,设AB: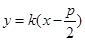 由
由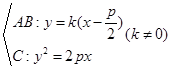 所以
所以 ,
,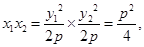 是定值(2)
是定值(2)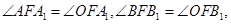
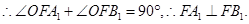
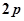 ,证明:
,证明: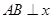 时
时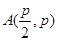 、
、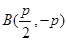 ,
,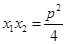 、
、 ,是定值;AB与x轴不垂直时,设AB:
,是定值;AB与x轴不垂直时,设AB: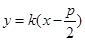 由
由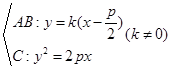 所以
所以 ,
,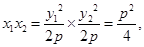 是定值(2)
是定值(2)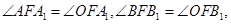
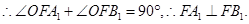
试题分析:焦点
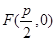 ,准线
,准线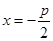
(1)
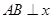 时
时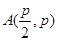 、
、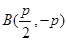 ,通径
,通径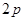 ,
,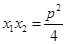 、
、 ,是定值.
,是定值.AB与x轴不垂直时,设AB:
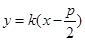 由
由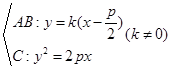 得
得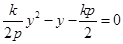 ,所以
,所以 ,
,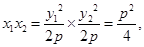 是定值.
是定值.(2)
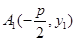 、
、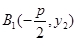 ,
,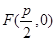
所以
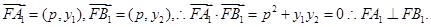
方法二:由抛物线知:
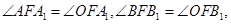
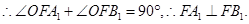
点评:直线与圆锥曲线相交时,联立方程利用韦达定理是常用的方法

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 .
.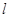 :y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.
:y=kx+m(m≠0)与(Ⅰ)中的轨迹C交于不同的两点A,B.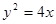 上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△MPF的面积( )
上一点P引抛物线准线的垂线,垂足为M,且|PM|=5,设抛物线的焦点为F,则△MPF的面积( )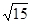
 中,两个定点
中,两个定点 ,
,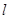 交动点C的轨迹于P、Q两点,求
交动点C的轨迹于P、Q两点,求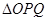 面积的最大值(O是坐标原点)。
面积的最大值(O是坐标原点)。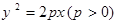 的焦点
的焦点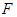 的直线与抛物线交于A、B两点,抛物线准线与x轴交于C点,若
的直线与抛物线交于A、B两点,抛物线准线与x轴交于C点,若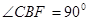 ,则|AF|-|BF|的值为( )
,则|AF|-|BF|的值为( )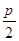 B.
B.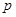 C.
C.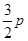 D.
D.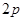
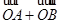 与
与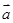 =(3,-1)共线.
=(3,-1)共线.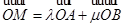 (
(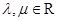 ),证明
),证明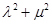 为定值.
为定值.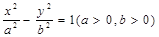 的离心率为e=
的离心率为e=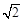 ,右焦点为F(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)
,右焦点为F(c,0),方程ax2-bx-c=0的两个实根分别为x1和x2,则点P(x1,x2)  围成的三角形区域(包含边界)为E,P(x,y)为该区域的一个动点,则目标函数z=x-2y的最小值为________.
围成的三角形区域(包含边界)为E,P(x,y)为该区域的一个动点,则目标函数z=x-2y的最小值为________.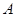 、
、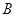 两个岛屿,
两个岛屿,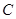 ,曾有渔船在距
,曾有渔船在距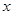 轴,
轴,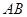 的垂直平分线为
的垂直平分线为 轴建立平面直角坐标系。
轴建立平面直角坐标系。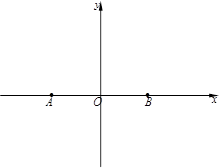
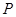 处反射信号的时间比为
处反射信号的时间比为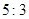 ,问你能否确定
,问你能否确定