题目内容
【题目】设关于x的二次方程px2+（p﹣1）x+p+1=0有两个不相等的正根，且一根大于另一根的两倍，求p的取值范围．
【答案】解：关于x的二次方程px2+（p﹣1）x+p+1=0有两个不相等的正根，
则△=（p﹣1）2﹣4p（p+1）=﹣3p2﹣6p+1＞0，解得﹣1﹣ 
＜p＜﹣1+ ，
当x1+x2= 
＞0，及x1x2= 
＞0时，方程的两根为正．解之，得0＜p＜1．故0＜p＜ ﹣1．
记x1= 
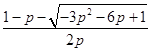，x2=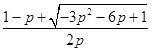 
，
由x2＞2x1，并注意p＞0，得3 
＞1﹣p＞0，
∴28p2+52p﹣8＜0，即7p2+13p﹣2＜0．∴﹣2＜p＜ 
．
综上得p的取值范围为{p|0＜p＜ }
【解析】根据根与系数的关系和判别式即可求出p的范围．
练习册系列答案
相关题目
【题目】某产品的三个质量指标分别为x，y，z，用综合指标S＝x＋y＋z评价该产品的等级．若S≤4, 则该产品为一等品．先从一批该产品中，随机抽取10件产品作为样本，其质量指标列表如下：
产品编号 | A1 | A2 | A3 | A4 | A5 |
质量指标 (x, y, z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
产品编号 | A6 | A7 | A8 | A9 | A10 |
质量指标 (x, y, z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(1)利用上表提供的样本数据估计该批产品的一等品率；
(2)在该样本的一等品中， 随机抽取2件产品，
(ⅰ) 用产品编号列出所有可能的结果；
(ⅱ) 设事件B为“在取出的2件产品中， 每件产品的综合指标S都等于4”， 求事件B发生的概率．
