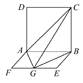
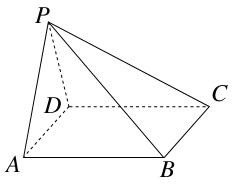
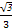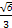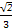题目内容
如图,在直三棱柱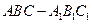 中,
中,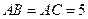 ,
,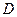 ,
,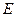 分别为
分别为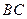 ,
,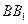 的中点,四边形
的中点,四边形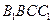 是边长为
是边长为 的正方形.
的正方形.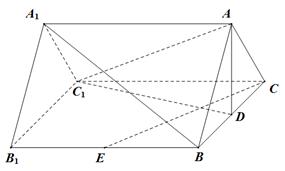
(Ⅰ)求证: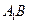 ∥平面
∥平面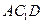 ;
;
(Ⅱ)求证: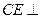 平面
平面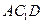 ;
;
(Ⅲ)求二面角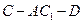 的余弦值.
的余弦值.
(Ⅰ)证明:连结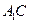 ,与
,与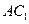 交于
交于 点,连结
点,连结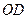 .因为
.因为 ,
,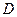 分别为
分别为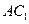 和
和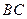 的中点,所以
的中点,所以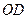 ∥
∥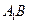 .又
.又 平面
平面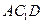 ,
,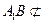 平面
平面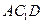 ,
,
所以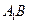 ∥平面
∥平面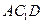 . ……………………4分
. ……………………4分
(Ⅱ)证明:在直三棱柱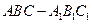 中,
中, 平面
平面 ,又
,又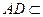 平面
平面 ,所以
,所以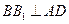 .因为
.因为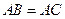 ,
,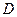 为
为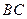 中点,所以
中点,所以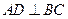 .又
.又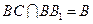 ,
,
所以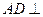 平面
平面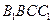 .又
.又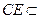 平面
平面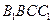 ,所以
,所以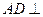
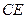 .
.
因为四边形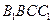 为正方形,
为正方形,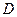 ,
,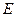 分别为
分别为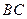 ,
,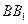 的中点,
的中点,
所以 △
△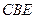 ≌
≌ △
△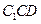 ,
,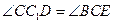 . 所以
. 所以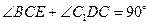 .
.
所以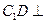
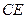 .
.
又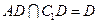 ,所以
,所以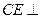 平面
平面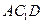 . ……………………8分
. ……………………8分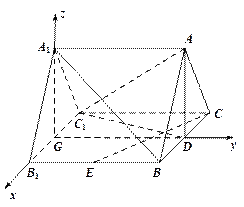
(Ⅲ)解:如图,以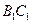 的中点
的中点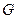 为原点,建立空间直角坐标系.
为原点,建立空间直角坐标系.
则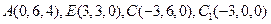 .
.
由(Ⅱ)知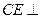 平面
平面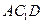 ,所以
,所以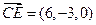 为平面
为平面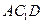 的一个法向量.
的一个法向量.
设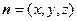 为平面
为平面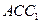 的一个法向量,
的一个法向量,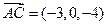 ,
,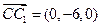 .
.
由 可得
可得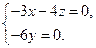
令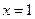 ,则
,则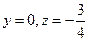 .
.
所以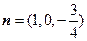 .
.
从而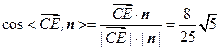 .
.
因为二面角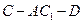 为锐角,
为锐角,
所以二面角
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在如图所示的空间直角坐标系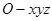 中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2),给出编号①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )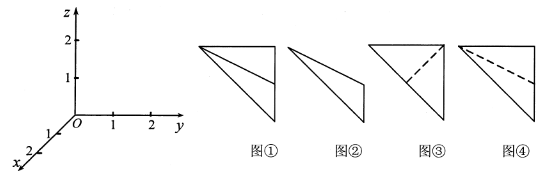
| A.①和② | B.③和① | C.④和③ | D.④和② |
已知正方体ABCD-A1B1C1D1中,点E为上底面A1C1的中心,若 =
= +x
+x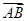 +y
+y ,则x、y的值分别为( )
,则x、y的值分别为( )
| A.x=1,y=1 | B.x=1,y=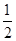 |
C.x=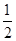 ,y= ,y=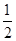 | D.x=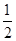 ,y=1 ,y=1 |
 中,
中, ,
,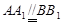 ,
, ,
, 。
。
 ;
; ;
; 的余弦值。
的余弦值。 中,已知
中,已知 ,
, .
. ;
; 是
是 上一点,试确定
上一点,试确定 平面
平面 ,并证明.
,并证明.
 ,AA1=4,点D是AB的中点
,AA1=4,点D是AB的中点 AC⊥BC1;
AC⊥BC1; 的平面角的正切值.
的平面角的正切值.
 B=1,BC=a,PA⊥平面ABCD
B=1,BC=a,PA⊥平面ABCD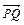 ⊥
⊥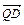 ,说明理由.
,说明理由.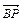 ,
,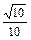 时,求点P的位置.
时,求点P的位置.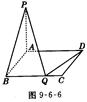
 AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )