题目内容
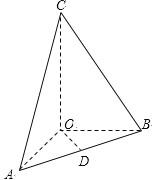
【题目】如图,平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 边的中点,沿
边的中点,沿![]() 将
将![]() 折起使得平面
折起使得平面![]() 平面
平面![]() .
.
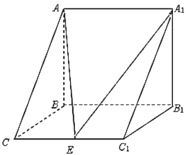
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积;
的体积;
(3)求折后直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
(1)根据面面垂直的性质定理,证得![]() 平面
平面![]() ,由此证得平面
,由此证得平面![]() 平面
平面![]() .
.
(2)![]() 的中点
的中点![]() ,根据等比三角形的性质得到
,根据等比三角形的性质得到![]() 由面面垂直的性质定理得
由面面垂直的性质定理得![]() 平面
平面![]() ,也即
,也即![]() 是四棱锥
是四棱锥![]() 的高.进而求得四棱锥
的高.进而求得四棱锥![]() 的体积.
的体积.
(3)以![]() 为空间坐标系原点建立空间直角坐标系,利用直线
为空间坐标系原点建立空间直角坐标系,利用直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,计算出直线
的法向量,计算出直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
(1)证明:∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
由题易知![]() ,且
,且![]() 平面
平面![]() .
.
∴![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(2)由已知有![]() 是正三角形,取
是正三角形,取![]() 的中点
的中点![]() ,则
,则![]() ,又平面
,又平面![]() 平面
平面![]() 于
于![]() ,
,
则![]() 平面
平面![]() ,且
,且![]() ,
,
易求得![]() ,
,
∴![]() .
.
(3)作![]() ,由(1)知可如图建系,
,由(1)知可如图建系,
则![]() ,
,![]() ,
,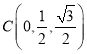 ,
,
![]() ,
,
又![]() ,得
,得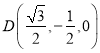 ,
,
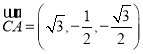 ,
,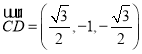 .
.
设平面![]() 的法向量
的法向量![]() ,则
,则
 ,不妨取
,不妨取![]() .
.
设折后直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,则
,则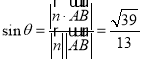 .
.


练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
【题目】某高新企业自2012年成立以来,不断创新技术与产品,积极拓展市场,销售收入![]() (单位万元)与年份代号
(单位万元)与年份代号![]() 之间对应关系如下表,且满足回归函数
之间对应关系如下表,且满足回归函数![]() ,记
,记![]() 。
。
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
销售收入 | 80 | 199 | 398 | 2512 | 6310 | 15848 | 79432 |
| 1.9 | 2.3 | 2.6 | 3.4 | 3.8 | 4.2 | 4.9 |
(1)任取2年对比销售收入的情况,求这2年中销售收入均超过400万元的概率;
(2)求回归函数![]() 中
中![]() 的值。
的值。
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
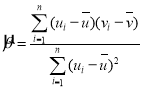 ,
,![]()