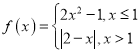题目内容
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间和极值;
的单调区间和极值;
(2)若![]() ,试讨论函数
,试讨论函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;函数
;函数![]() 在
在![]() 处取的极小值
处取的极小值![]() ,无极大值;(2)见解析.
,无极大值;(2)见解析.
【解析】
(1)求出导函数![]() ,由
,由![]()
![]() 确定增区间,
确定增区间,![]()
![]() 确定减区间,得极值;
确定减区间,得极值;
(2)求出导函数![]() ,分类讨论,利用导数研究函数的单调性与极值,根据零点存在定理得零点个数.
,分类讨论,利用导数研究函数的单调性与极值,根据零点存在定理得零点个数.
(1)根据![]() ,
,
令![]() ,解得
,解得![]() ,当
,当![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
x |
| -1 |
|
| <0 | 0 | >0 |
| 递减 |
| 递增 |
∴函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() ;
;
函数![]() 在
在![]() 处取的极小值
处取的极小值![]() ,无极大值.
,无极大值.
(2)由![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,易知函数
,易知函数![]() 只有一个零点,
只有一个零点,
当![]() 时,在
时,在![]() 上
上![]() ,
,![]() 单调递减;在
单调递减;在![]() 上
上![]() ,
,![]() 单调递增,又
单调递增,又![]() ,当
,当![]() 时,
时,![]() ,
,
所以函数![]() 有两个零点,
有两个零点,
当![]() 时,在
时,在![]() 和
和![]() 上
上![]() ,
,![]() 单调递增,在
单调递增,在![]() 上
上![]() ,
,![]() 单调递减.又
单调递减.又![]() ,
,
且当![]() 时,
时,![]() 所以函数
所以函数![]() 有一个零点
有一个零点

练习册系列答案
相关题目
【题目】为发挥体育咋核心素养时代的独特育人价值,越来越多的中学生已将某些体育项目纳入到学生的必修课程,某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生抽取了100人进行调查.
班 级 | 一(1) | 一(2) | 一(3) | 一(4) | 一(5) | 一(6) | 一(7) | 一(8) | 一(9) | 一(10) |
市级比赛 获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
市级以上比 赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
(1)已知在被抽取的女生中有6名高一(1)班学生,其中3名对游泳有兴趣,现在从这6名学生中最忌抽取3人,求至少有2人对游泳有兴趣的概率;
(2)该研究性学习小组在调查发现,对游泳有兴趣的学生中有部分曾在市级以上游泳比赛中获奖,如上表所示,若从高一(8)班和高一(9)班获奖学生中随机各抽取2人进行跟踪调查.记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.