题目内容
【题目】已知关于x的不等式
的解集为
．
（1）求a，b的值．
（2）当
时，解关于x的不等式
．
【答案】（1）
（2）见解析
【解析】
试题
(1)利用韦达定理可得
；
(2)结合(1)的结论分类讨论实数c的范围即可求得不等式的解集.
试题解析：
解：（1）因为不等式ax2－3x＋2>0的解集为{x|x<1或x>b}
所以x1＝1与x2＝b是方程ax2－3x＋2＝0的两个实数根
b>1且a>0
得
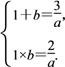解得
（2）不等式ax2－(ac＋b)x＋bc<0，
即x2－(2＋c)x＋2c<0，即(x－2)(x－c)<0.
当c>2时，不等式(x－2)(x－c)<0的解集为{x|2<x<c}；
当c<2时，不等式(x－2)(x－c)<0的解集为{x|c<x<2}；
当c＝2时，不等式(x－2)(x－c)<0的解集为
练习册系列答案
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
相关题目
【题目】某商场举行有奖促销活动，顾客购买一定金额的商品后即可参加一次抽奖.随着抽奖活动的有效开展，参与抽奖活动的人数越来越多，该商场对前5天抽奖活动的人数进行统计，y表示第x天参加抽奖活动的人数，得到统计表如下：
x | 1 | 2 | 3 | 4 | 5 |
y | 50 | 60 | 70 | 80 | 100 |
经过进一步统计分析，发现y与x具有线性相关关系.
（1）若从这5天随机抽取两天，求至少有1天参加抽奖人数超过70的概率；
（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程
，并估计该活动持续7天，共有多少名顾客参加抽奖？
参考公式及数据：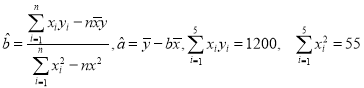
.
