题目内容
15．
如图，正方体ABCD-A1B1C1D1的棱长为2．（1）证明：AC⊥B1D；
（2）求三棱锥C-BDB1的体积．
分析 （1）证明AC⊥平面BB1D，即可证明AC⊥B1D；
（2）利用等体积转化求三棱锥C-BDB1的体积．
解答 证明：（1）∵ABCD-A1B1C1D1是正方体，
∴BB1⊥平面ABCD，
∵AC?平面ABCD，
∴BB1⊥AC，
∵AC⊥BD，BB1∩BD=B，
∴AC⊥平面BB1D，
∵B1D?平面BB1D，
∴AC⊥B1D，
（2）解：∵BB1⊥平面ABCD，
∴BB1是三棱锥B1-BDC的高，
∴${V}_{C-BD{B}_{1}}$=${V}_{{B}_{1}-BDC}$=$\frac{1}{3}×\frac{1}{2}×2×2×2$=$\frac{4}{3}$．
点评 本题考查线面垂直的证明，考查三棱锥体积的计算，利用等体积转化是关键．
练习册系列答案
相关题目
5．定义域为R的函数f（x）满足f（x+1）=2f（x），当x∈[0，2）时，f（x）=$\left\{\begin{array}{l}{{x}^{2}-x，x∈[0，1）}\\{lo{g}_{\sqrt{2}}（x+1），x∈[1，2）}\end{array}\right.$，若x∈[-2，0）时，对任意的t∈[1，2]都有f（x）≥$\frac{t}{16}$-$\frac{a}{8{t}^{2}}$成立，则实数a的取值范围是（ ）
| A． | （-∞，6） | B． | [6，+∞） | C． | （-∞，6] | D． | （-∞，12] |
如图，边长为2的正方形ABCD中，点E，F分别在线段AB与BC上，且满足：BE=BF=$\frac{1}{2}$BC，将△AED，△DCF分别沿DE，DF折起，使A，C两点重合于点P，并连结PB．
10．已知等比数列{an}的各项均为正数，且公比q≠1，若a4、a5、2a3成等差数列，则公比q=（ ）
| A． | $\frac{1+\sqrt{3}}{2}$或$\frac{1-\sqrt{3}}{2}$ | B． | $\frac{1+\sqrt{17}}{4}$ | C． | $\frac{1+\sqrt{5}}{2}$或$\frac{1-\sqrt{5}}{2}$ | D． | $\frac{1+\sqrt{5}}{2}$ |
20．
已知三棱锥A-BCD的侧面展开图放在正方形网格（横、纵的单位长度均为1）中的位置如图所示，那么其体积是（ ）
已知三棱锥A-BCD的侧面展开图放在正方形网格（横、纵的单位长度均为1）中的位置如图所示，那么其体积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | 4 |
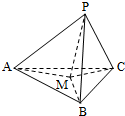如图，在三棱锥P-ABC中，PA、PB、PC两两垂直，且PA=3，PB=2，PC=1．设M是底面ABC内一点，定义f（M）=（m，n，p），其中m、n、P分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积．若f（M）=（$\frac{1}{2}$，x，y），且$\frac{1}{x}$+$\frac{a}{y}$≥18恒成立，则正实数a的最小值为4．
4．设函数f（x）在R上存在导数f′（x），?x∈R，有f（-x）+f（x）=x2，在（0，+∞）上f′（x）＜x，若f（4-m）-f（m）≥8-4m．则实数m的取值范围为（ ）
| A． | [-2，2] | B． | [2，+∞） | C． | [0，+∞） | D． | （-∞，-2]∪[2，+∞） |