题目内容
3.已知:不等式组$\left\{\begin{array}{l}{{x}^{2}-2x+{y}^{2}≥0}\\{1≤x≤2}\\{-1≤y≤1}\end{array}\right.$所表示的平面区域为Ω,P(x1,y1),Q(x2,y2)是Ω内任意一点,则z=(x1-1)(x2-1)+y1y2的最大值是2.分析 画出不等式组表示的可行域,化简所求表达式利用基本不等式求解最值.
解答  解:不等式组$\left\{\begin{array}{l}{{x}^{2}-2x+{y}^{2}≥0}\\{1≤x≤2}\\{-1≤y≤1}\end{array}\right.$转化为:$\left\{\begin{array}{l}{(x-1)}^{2}+{y}^{2}≥1\\ 1≤x≤2\\-1≤y≤1\end{array}\right.$,如图:
解:不等式组$\left\{\begin{array}{l}{{x}^{2}-2x+{y}^{2}≥0}\\{1≤x≤2}\\{-1≤y≤1}\end{array}\right.$转化为:$\left\{\begin{array}{l}{(x-1)}^{2}+{y}^{2}≥1\\ 1≤x≤2\\-1≤y≤1\end{array}\right.$,如图:
P(x1,y1),Q(x2,y2)是Ω内任意一点,则z=(x1-1)(x2-1)+y1y2,
∵-1≤y≤1,∴y1y2≤1,∵x1+x2≥2$\sqrt{{x}_{1}{x}_{2}}$.
z=(x1-1)(x2-1)+y1y2=y1y2+1+x1x2-(x1+x2)
≤2+x1x2-2$\sqrt{{x}_{1}{x}_{2}}$
=$(\sqrt{{x}_{1}{x}_{2}}-1)^{2}+1$.
x1x2≤4.
$1≤\sqrt{{x}_{1}{x}_{2}}≤2$.
z≤2.
∴z=(x1-1)(x2-1)+y1y2的最大值是2.
故答案为2
点评 本题考查线性规划的应用,考查基本不等式以及线性规划,考查分析问题解决问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
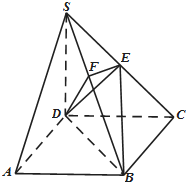 如图,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥底面ABCD,SD=DC=2,E是SC的中点,作EF⊥SB交SB于F.
如图,在四棱锥S-ABCD中,底面ABCD是正方形,侧棱SD⊥底面ABCD,SD=DC=2,E是SC的中点,作EF⊥SB交SB于F. 如图,正方体ABCD-A1B1C1D1的棱长为2.
如图,正方体ABCD-A1B1C1D1的棱长为2.