题目内容
20．
已知三棱锥A-BCD的侧面展开图放在正方形网格（横、纵的单位长度均为1）中的位置如图所示，那么其体积是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{2}{3}$ | C． | $\frac{4}{3}$ | D． | 4 |
分析 由题意，△ACD是等腰直角三角形，其面积为$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1，BC=BA=BD=$\sqrt{5}$，B在平面ACD中的射影是CD的中点O，即可求出三棱锥A-BCD的体积．
解答 解：由题意，△ACD是等腰直角三角形，其面积为$\frac{1}{2}×\sqrt{2}×\sqrt{2}$=1，
BC=BA=BD=$\sqrt{5}$，B在平面ACD中的射影是CD的中点O，∴BO=$\sqrt{5-1}$=2，
∴VA-BCD=VB-ACD=$\frac{1}{3}×1×2$=$\frac{2}{3}$．
故选：B．
点评 本题考查三棱锥A-BCD的体积，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
如图，棱长为a的正方体ABCD-A1B1C1D1中，点E、F、G分别为CD1、A1B1、B1C1的中点，则三棱锥A-EFG的体积为$\frac{{a}^{3}}{16}$．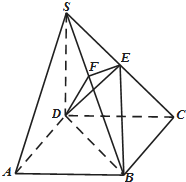
如图，在四棱锥S-ABCD中，底面ABCD是正方形，侧棱SD⊥底面ABCD，SD=DC=2，E是SC的中点，作EF⊥SB交SB于F．
如图，正方体ABCD-A1B1C1D1的棱长为2．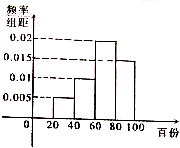
某大型连锁超市为迎接春节购物季，销售一批年货产品，已知每销售1份获利30元，未销售的产品每份损失10元，根据以往销售情况其市场需求量的频率分布直方图如图所示，该超市欲购8000份．
如图，抛物线C1：y2=4x的焦准距（焦点到准线的距离）与椭圆C2：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的长半轴相等，设椭圆的右顶点为A，C1，C2在第一象限的交点为B，O为坐标原点，且△OAB的面积为$\frac{{2\sqrt{6}}}{3}$